Криптографические алгоритмы
(по материалам открытой печати)
Шифр Ривеста — Шамира — Алдемана (RSA)
Цифровая подпись от Эль-Гамаля
Доказательство при нулевом знании
До 60-70 годов XX века криптография развивалась во всех странах под эгидой ведомств, отвечающих за безопасность связи и информации. С совершенствованием средств связи, таких как телеграф, телефон, радио, менялся характер криптографии, а применение электронных средств передачи информации усложнило и расширило задачи криптографии. С широким распространением компьютерных технологий проблематика криптографии преобразилась и пополнилась многочисленными задачами, не связанными непосредственно с засекречиванием информации, — разработка систем электронной цифровой подписи и электронных протоколов выборов; подписание контракта и идентификация удаленных пользователей; методы защиты от навязывания ложных сообщений и систем электронных платежей.
Значение криптографии в жизни общества продолжает возрастать. Недаром Дэвид Кан, автор фундаментального труда «Взломщики кодов», утверждал: «Великая держава — это страна, которая владеет ядерными технологиями, ракетной техникой и криптографией». Не менее важную роль отводит криптографии и Ривест, один из авторов системы шифра RSA: «Криптография — это повивальная бабка всех компьютерных наук». Еще ярче выразились авторы книги «Абстрактная прикладная алгебра» Р.Лидл и Г.Пильц: «Современная криптография может быть охарактеризована и как важная дорогостоящая проблема, и как раздел прикладной математики». Здесь под первой проблемой подразумевается проблема получения доказуемых нижних оценок стойкости шифров, а в математическом плане это один из частных случаев фундаментальной проблемы нижних оценок сложности алгоритмов.
Понимание математического характера криптографии началось с работ К.Шеннона. Его труд «Математическая теория криптографии» в секретном варианте появился в 1945 году, а рассекречен и опубликован был в США в 1949-м. В 1963 году по инициативе А.Н.Колмогорова сборник работ К.Шенона был издан и на русском языке. В 60-х годах были рассекречены и опубликованы результаты исследований немецкого шифратора «Энигма» и связанные с его вскрытием результаты по решению уравнений в подстановках.
В 70-х годах была опубликована революционная работа «Новые направления в криптографии» молодых американских ученых У.Диффи (Diffie) и М.Хеллмана (Hellman). С этого времени количество публикаций по криптографии стало стремительно увеличиваться. Это объясняется разными причинами: с одной стороны, постоянное расширение областей применения криптографии; с другой — новизна и привлекательность для ученых математических моделей и задач, которые возникают из потребностей криптографии. И наконец, именно в это время сформировались все атрибуты криптографии как науки: возникли направления и научные школы со своей внутренней логикой развития, появились специализированные международные журналы, сложилась практика ежегодного проведения международных конференций.
С 70-х годов сфера применения криптографии начала расширяться, криптография стала гражданской отраслью, то есть криптографические средства начали применяться для защиты коммерческой информации. Именно для этой цели в США в 1978 году был принят стандарт алгоритма шифрования данных DES, являющийся блочным шифром с длиной блока 64 бит.
В настоящее время все развитые страны имеют свои стандарты шифрования. Идет постоянная борьба различных криптографических алгоритмов за признание их в качестве международного стандарта шифрования. В то же время У.Диффи и М.Хеллман предложили использовать так называемые системы с открытыми ключами для систем связи, где нет возможности для скрытого распространения ключей, но возможен двусторонний обмен информацией. Фиксированная процедура такого обмена позволяет выработать общий секретный ключ. В этот период было предложено несколько систем с открытыми ключами. Среди них — система RSA, названная так по первым буквам ее создателей — Райвеста (Rivest), Шамира (Shamir) и Адлемана (Adleman). В системе открытые сообщения кодируются натуральными числами, а операция шифрования заключается в возведении в степень числа, представляющего открытый текст, и в приведении полученного числа по некоторому модулю. Дешифрование данной системы представляет собой известную математическую задачу дискретного логарифмирования, для которой к настоящему моменту не найдено эффективных алгоритмов решения.
Другая система — система Меркля — Хеллмана (Merkle — Hellman) основана на математической проблеме «о рюкзаке», заключающейся в представлении натурального числа в виде суммы чисел из множества заданных. Труднорешаемость задачи дешифрования этой системы основана на так называемых NP-полных проблемах.
При потоковом (симметрическом) шифровании каждый знак шифртекста (ШТ) является функцией значения и положения знака открытого текста (ОТ). Знаками бывают биты, байты и редко — более крупные единицы текста. Этот вид шифрования реализуется на обоих концах линии связи с помощью одинаковых или почти одинаковых шифровальных устройств (шифраторов). Симметрическое шифрование является сейчас наиболее распространенным и представляет собой шифр замены. Заметим, что 25 лет назад асимметрических систем шифрования еще не было — все системы шифрования были симметрическими.
При блочном (асимметрическом) шифровании ОТ разбивается на равные по длине блоки бит. К блокам применяется зависящая от ключа функция шифрования для преобразования их в блоки ШТ такой же длины. Обычно блоки шифруются взбиванием (перестановкой).
В системах с открытым ключом знания ключа шифрования не достаточно для расшифрования, и наоборот. Системы с открытым ключом всегда блочные. Асимметрическое шифрование принципиально отличается от симметрического тем, что его алгоритм, представляющий собой отображение некоторого множества на себя, является общеизвестным. Стойкость этого шифрования основывается на том, что злоумышленник (нелегальный пользователь) не в состоянии доступными ему средствами вычислить обратное отображение. Вместе с тем вычисление обратного отображения для легального пользователя доступно благодаря тому, что он знает секрет, который был использован при построении прямого отображения.
Еще один подтип алгоритмов шифрования — шифрование со сверткой. Если в потоковом и блочном шифре функция шифрования зависит от ключа, то в шифрах со сверткой она зависит как от ключа, так и от одного или более предшествующих символов или блоков текста.
Традиционно стойкость шифратора — это число операций, необходимых для определения его ключа при некоторых предположениях. В первом предположении считается, что противник знает устройство шифратора, но не его ключ. Ему также известно некоторое число знаков, выработанное шифратором на данном ключе, то есть ШТ.
Теоретическое открытие, оказавшее существенное влияние на развитие криптографии, было сделано в работе «Теория связи в секретных системах» К.Шеннона, опубликованной в 1949 году. В ней сформулированы и доказаны необходимые и достаточные условия стойкости системы шифра. Они заключаются в том, что получение злоумышленником шифртекста не изменяет вероятностей используемых ключей. При этом было установлено, что единственным таким шифром является так называемая лента одноразового использования, когда открытый текст шифруется с помощью случайного ключа такой же длины. Это обстоятельство делает стойкий шифр очень дорогим в эксплуатации.
Поэтому основная проблема криптографии — трудность генерирования непредсказуемых двоичных последовательностей большой длины с применением короткого случайного ключа. Для ее решения используются генераторы двоичных псевдослучайных последовательностей. Получаемые программно из ключа псевдослучайные ряды чисел или бит называются гаммой. Стойким считается генератор:
- с большим периодом (повторяемость знаков) ряда;
- равновероятностью знаков в ряде;
- простым способом получения знаков.
Подавляющее
большинство генераторов порождает
детерминированные рекуррентные
последовательности
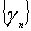 большого, но
конечного периода. Примерами соотношений,
определяющих такие последовательности,
являются:
большого, но
конечного периода. Примерами соотношений,
определяющих такие последовательности,
являются:
-
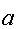 — конгруэнтный генератор (впервые предложенный
Д.Х.Лемером). Рекуррентные последовательности с простыми функциональными зависимостями
между знаками обладают рядом свойств регулярности, которые обнаруживаются
даже на их сравнительно коротких отрезках, что может быть допустимо в вычислительных
алгоритмах и процедурах статистического моделирования, но для криптографии
неприемлемо. При вычислении в целых числах для значений
— конгруэнтный генератор (впервые предложенный
Д.Х.Лемером). Рекуррентные последовательности с простыми функциональными зависимостями
между знаками обладают рядом свойств регулярности, которые обнаруживаются
даже на их сравнительно коротких отрезках, что может быть допустимо в вычислительных
алгоритмах и процедурах статистического моделирования, но для криптографии
неприемлемо. При вычислении в целых числах для значений 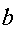
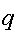 наибольший период
наибольший период 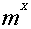 достигается
при
достигается
при 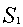 или
или 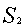 и нечетном начальном
числе.
и нечетном начальном
числе. - 2. Генераторы, основанные на использовании последовательности Фибоначчи
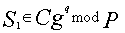 , вычисляемой по формулам
, вычисляемой по формулам
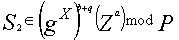 .
. Механизм образования гаммы может быть различным, например выбирается последняя цифра каждого числа из последовательности Фибоначчи и получается множество
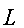 . Последовательность может использоваться для начального
заполнения массива большой длины. Другой вариант — генераторы с запаздыванием,
у которых складываются не соседние, а удаленные числа. Генераторы такого
типа могут быть использованы как «усилители случайности». Причем период
выходной последовательности таких генераторов значительно больше, чем у
конгруэнтных генераторов.
. Последовательность может использоваться для начального
заполнения массива большой длины. Другой вариант — генераторы с запаздыванием,
у которых складываются не соседние, а удаленные числа. Генераторы такого
типа могут быть использованы как «усилители случайности». Причем период
выходной последовательности таких генераторов значительно больше, чем у
конгруэнтных генераторов. - 3. Еще один тип генераторов — генераторы, основанные на рекуррентной двоичной
последовательности. Если сложность последовательности
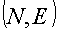 равна
равна 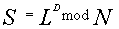 , то любые
, то любые 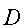 последовательные ее значения зависимы. Если эта зависимость линейная, то мы
имеем рекуррентное соотношение:
последовательные ее значения зависимы. Если эта зависимость линейная, то мы
имеем рекуррентное соотношение: 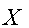 , где
коэффициенты
, где
коэффициенты 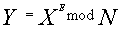 . По начальным данным
. По начальным данным 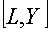 длины
длины 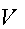 , которые можно рассматривать
как ключ или часть ключа шифра, строится бесконечная последовательность. Каждый
последующий член определяется из
, которые можно рассматривать
как ключ или часть ключа шифра, строится бесконечная последовательность. Каждый
последующий член определяется из 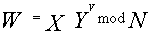 предыдущих
членов. Особенно просто реализовать рекуррентную двоичную последовательность,
если
предыдущих
членов. Особенно просто реализовать рекуррентную двоичную последовательность,
если 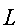 и
и 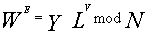 . На множестве таких чисел определены операции сложения и умножения, то есть
имеется поле из двух элементов, которое обозначается как GF(2) — поле Галуа.
GF(n) — обозначение для поля с
. На множестве таких чисел определены операции сложения и умножения, то есть
имеется поле из двух элементов, которое обозначается как GF(2) — поле Галуа.
GF(n) — обозначение для поля с 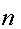 элементами.
Для того чтобы знаки гаммы получались равновероятными и имели большой период,
элементами.
Для того чтобы знаки гаммы получались равновероятными и имели большой период,
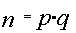 должно быть простым числом. Табличное
представление операций сложения и умножения показано на рис.
1.
должно быть простым числом. Табличное
представление операций сложения и умножения показано на рис.
1.
Схема деления данных в поле из 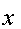 бит на
полином
бит на
полином  представлена на рис.
2.
представлена на рис.
2.
Данные сдвигаются влево на один бит (ячейку). В освобождающийся крайний правый
бит записывается сумма элементов заполнения по модулю два, умноженных на соответствующие
коэффициенты многочлена  . В результате
операции получаем многочлен
. В результате
операции получаем многочлен 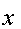 .
.
Таким образом, достигается связь между линейными рекуррентными последовательностями, делением многочленов над полем GF(2) и алгоритмом получения бесконечной псевдослучайной последовательности. Часто, особенно в отечественной литературе, вышеприведенная схема называется одноканальной линией задержки (ОЛЗ).
Рассмотрим получение последовательности на примере рекуррентного соотношения
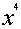 , для которого
, для которого 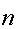 — соответствующий неприводимый многочлен. Многочлен порождает расширение GF(8).
Мультипликативная группа в GF(8) имеет семь элементов и циклична в силу простоты
числа 7. Электронная схема представлена на рис. 3.
— соответствующий неприводимый многочлен. Многочлен порождает расширение GF(8).
Мультипликативная группа в GF(8) имеет семь элементов и циклична в силу простоты
числа 7. Электронная схема представлена на рис. 3.
Результат выполнения алгоритма получения псевдослучайной последовательности представлен в табл. 1 и 2.
Во втором столбце табл. 2 показаны различные варианты получаемой последовательности, то есть гаммы, для различных вариантов начальных заполнений, приведенных в первом столбце той же таблицы. Табл. 1 демонстрирует движение данных в процессе работы ОЛЗ для выделенного жирным шрифтом в табл. 2 варианта начального заполнения. Пример является вырожденным, так как длина периода получаемой последовательности мала. Выбор рекуррентного соотношения большей длины с соответствующими точками съема и одновременное использование нескольких ОЛЗ дают выходные последовательности с большим периодом. Поэтому такой алгоритм получения гаммы используется в большинстве современных шифраторов.
В 1976 году У.Диффи и М.Хеллман предложили новый вид организации связи без предварительного снабжения абонентов секретными ключами — так называемое шифрование с открытым ключом. В своей работе К.Шеннон предлагал «строить шифр таким образом, чтобы его раскрытие было эквивалентно решению математической задачи, требующей выполнения объемов вычислений, превосходящих возможности современных компьютеров». Именно этот принцип используют все системы шифрования с открытым ключом. Нельзя уверенно сказать, что сообщения, зашифрованные такими способами шифрования, никто не может прочесть. Но можно утверждать, что тот, кто читает эти сообщения, достаточно богат, так как может позволить себе создание дорогостоящих вычислительных установок с высокой производительностью, либо знает все тонкости применения сетевых технологий, позволяющих временно объединять для решения одной задачи сотни тысяч компьютеров.
Все системы шифрования с открытым ключом, помимо алгоритмической части, то есть способа наложения гаммы или способа перемешивания, имеют протокольную часть — порядок обмена сообщениями, необходимый для установления секретной связи.
Рассмотрим наиболее часто используемые системы шифрования с открытым ключом, применение которых часто выходит за рамки простого шифрования информации.
Шифр Ривеста — Шамира — Алдемана (RSA)
- Выбираются два очень больших простых числа
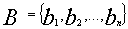 и
и 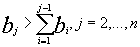 , вычисляются
, вычисляются 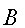 ;
; 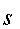 .
. - Выбирается случайное число
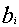 , взаимно
простое с
, взаимно
простое с 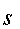 , и вычисляется
, и вычисляется 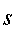 , удовлетворяющее условию
, удовлетворяющее условию 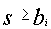
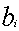 .
. 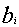 и
и 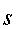 публикуются как свой открытый ключ шифрования, сохраняя
публикуются как свой открытый ключ шифрования, сохраняя 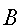 как секретный ключ.
как секретный ключ. - Если
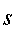 — сообщение, длина которого
определяется по значению выражаемого им целого числа и должна быть в интервале
— сообщение, длина которого
определяется по значению выражаемого им целого числа и должна быть в интервале
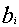 , то оно превращается в ШТ возведением
в степень
, то оно превращается в ШТ возведением
в степень 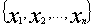 по модулю
по модулю 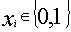 и отправляется получателю
и отправляется получателю 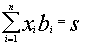 .
. - 5. Получатель расшифровывает
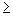 , возводя его в степень
, возводя его в степень
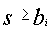 по модулю
по модулю
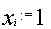
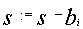 .
.
При P=211,
Q=223, N=47053,
M=46620
выбираем D=16
813. Если открытым текстом является строка S=’RSA’, а
буквы кодируются 5-битовым кодом (R=18, S=19,
A=1), то S=18+19*32+1*32*32=1650.
Тогда шифрование представляется формулой
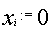 , а расшифровка
, а расшифровка
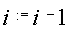 соответственно.
соответственно.
Время шифрования, расшифрования по алгоритму RSA в 1000 раз превышает алгоритм блочного шифрования DES. Но применение данного алгоритма шифрования добавляет новую функциональность в секретную переписку. После опубликования ключей любой абонент может зашифровать по общеизвестному алгоритму и отослать абоненту, опубликовавшему ключи, конфиденциальную информацию. При этом прочитать эту информацию сможет только владелец секретного ключа.
Шифр Эль-Гамаля
 1985 году был предложен алгоритм шифрования на основе возведения в степень большого
простого числа. Протокол шифра в варианте Шамира имеет следующий вид.
1985 году был предложен алгоритм шифрования на основе возведения в степень большого
простого числа. Протокол шифра в варианте Шамира имеет следующий вид.
1. Отправитель А и получатель В знают лишь большое простое число 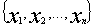 .
Генерируют случайные числа
.
Генерируют случайные числа 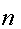 и
и 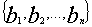 из интервала
из интервала 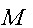 .
.
2.
А шифрует
сообщение
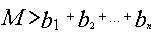 и высылает его В.
и высылает его В.
3.
В шифрует
его своим ключом
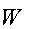 и высылает А.
и высылает А.
4.
А снимает
свой ключ
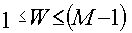 и возвращает
и возвращает
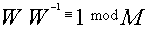 к В.
к В.
5. В расшифровывает 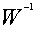 .
.
Если Р=11, Х=3, Y=2, S=4, то 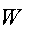 ,
, 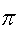 ,
, 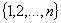 и, наконец,
и, наконец, 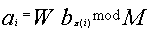 ,
то есть исходное сообщение.
,
то есть исходное сообщение.
Как и в предыдущем случае, применение данного алгоритма шифрования добавляет новую функциональность в секретную переписку.
Этот
алгоритм можно применять для игры в очко по
телефону, при этом игроки могут быть
уверены, что подтасовки не будет. Шифр
Гамаля имеет большую степень защиты,
чем шифр RSA.
В то же время если число
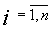 раскрыто, то
существует угроза для всех абонентов, в
отличие от алгоритма RSA.
раскрыто, то
существует угроза для всех абонентов, в
отличие от алгоритма RSA.
Открытое распределение ключей
 ротокол
этого шифра позволяет каждой паре пользователей системы выработать общий секретный
ключ. Алгоритмом Диффи — Хеллмана обеспечивается процедура предъявления пароля.
ротокол
этого шифра позволяет каждой паре пользователей системы выработать общий секретный
ключ. Алгоритмом Диффи — Хеллмана обеспечивается процедура предъявления пароля.
1.
Абоненты сети А и В, знают пару
открытых ключей
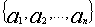 и
и
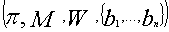 .
.
2.
Кроме того, у А есть секретный ключ
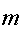 из интервала
из интервала
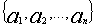 , а у В есть секретный ключ
, а у В есть секретный ключ
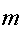 из того же
интервала.
из того же
интервала.
3.
Абонент А посылает В шифровку
своего ключа
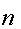 .
.
4.
Абонент В посылает А шифровку
своего ключа
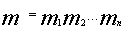 .
.
5. После этого общий ключ 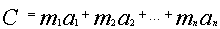 они вычисляют
по формуле
они вычисляют
по формуле 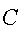 .
.
Время формирования общего ключа приблизительно в 5 раз меньше шифрования по алгоритму Эль-Гамаля и приблизительно в 30 раз меньше алгоритма RSA при том же уровне стойкости. Кроме того, можно легко расширить функциональность алгоритма на случай с тремя и более абонентами, одновременно работающими в сети.
Цифровая подпись от Эль-Гамаля
1.
Абоненты А и В знают
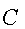 и случайное число
и случайное число
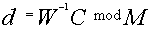 из интервала
из интервала
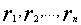 . А генерирует случайные числа
. А генерирует случайные числа
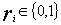 и
и
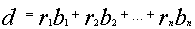 из того же
интервала.
из того же
интервала.
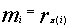 нужно хранить в секрете, а
нужно хранить в секрете, а
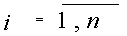 , являющееся открытым ключом, должно быть
взаимно простым с
, являющееся открытым ключом, должно быть
взаимно простым с
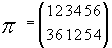 .
.
2.
А вычисляет
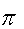 и
и
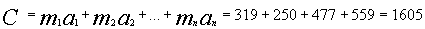 , решает относительно S
уравнение
, решает относительно S
уравнение
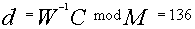 и передает В документ
с подписью
и передает В документ
с подписью
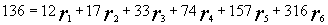 .
.
3. Получатель проверяет подпись, контролируя тождество 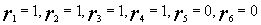 .
.
Или другой вариант шифра — цифровая подпись.
1.
Оба абонента знают:
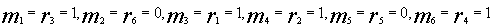 — общедоступное
большое простое число;
— общедоступное
большое простое число;
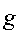 — примитивный
элемент.
— примитивный
элемент.
2.
А имеет
закрытый ключ
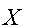 и открытый ключ
и открытый ключ
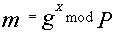 . Чтобы подписаться, А вычисляет
. Чтобы подписаться, А вычисляет
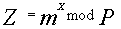
3.
В выбирает
случайное
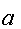 и
и
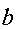 из
из
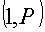 , вычисляет
, вычисляет
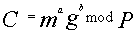 и посылает его А.
и посылает его А.
4.
А выбирает
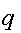 из
из
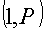 и отправляет к В
и отправляет к В
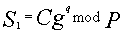 и
и
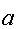 .
.
5.
В
посылает А
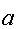 и
и
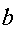
6. А посылает В 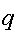 , чтобы он мог воспользоваться
, чтобы он мог воспользоваться
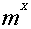 и восстановить
и восстановить 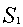 и
и 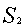 . Если
. Если 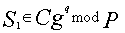 и
и 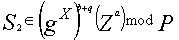 , то подпись правильна.
, то подпись правильна.
Основное назначение шифра «цифровая подпись» — не столько шифрование/расшифровка данных, сколько подписание любого электронного документа или идентификация удаленных пользователей.
Доказательство при нулевом знании
- А доказывает, В контролирует. Оба знают идентификатор
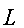 и открытый ключ
и открытый ключ 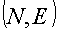 , но А, кроме того, знает
секретное число
, но А, кроме того, знает
секретное число 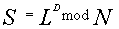 , где
, где 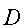 — секретный ключ.
— секретный ключ. - Сначала А генерирует случайное число
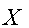 , вычисляет
, вычисляет 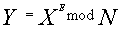 и отсылает
и отсылает 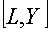 В.
В. - В генерирует и передает А случайное число
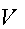 .
.
- А вычисляет и передает В
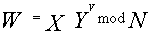 .
. - В проверяет принадлежность идентификатора
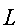 к А, контролируя тождество
к А, контролируя тождество 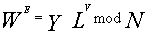 .
.
Извлечение
квадратных корней эквивалентно разложению
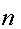 на множители.
на множители.
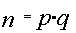 , причем абонент А знает сомножители
разложения, а абонент В — нет.
, причем абонент А знает сомножители
разложения, а абонент В — нет.
- В выбирает случайное число
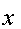 и сообщает
А значение
и сообщает
А значение  .
. - А сообщает В значение
 .
.
При этом В
не получает новой информации, так как сам
может возвести
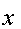 в квадрат. На шаге 2 А
не просто извлекает квадратный корень из
числа
в квадрат. На шаге 2 А
не просто извлекает квадратный корень из
числа
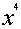 , а именно тот из них, который будет
квадратным вычетом по модулю
, а именно тот из них, который будет
квадратным вычетом по модулю
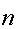 . Нахождение вычетов — трудно решаемая
математическая задача. На этом построена
стойкость алгоритма. Шифр-доказательство
при нулевом знании может быть использован
для организации методов защиты от
навязывания ложных сообщений и систем
электронных платежей наряду с шифром
цифровой подписи.
. Нахождение вычетов — трудно решаемая
математическая задача. На этом построена
стойкость алгоритма. Шифр-доказательство
при нулевом знании может быть использован
для организации методов защиты от
навязывания ложных сообщений и систем
электронных платежей наряду с шифром
цифровой подписи.
Задача о рюкзаке
Данный шифр представляет собой первую конкретную реализацию алгоритмов, использующих идею открытого ключа. Он основан на математической проблеме подбора, которая является NP-полной. Основная его идея заключается в том, чтобы выбрать математическую задачу, легкую (в вычислительном смысле) для решения, и замаскировать ее так, чтобы для непосвященных она оказалась трудной. Первоначальный набор рюкзака служит секретным ключом, а преобразованный набор рюкзака является открытым ключом.
Рюкзак — множество 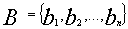 различных положительных
чисел. Элементы множества являются быстрорастущей последовательностью, удовлетворяющей
условию
различных положительных
чисел. Элементы множества являются быстрорастущей последовательностью, удовлетворяющей
условию 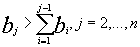 . Если имеется множество
. Если имеется множество 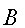 и положительное целое число
и положительное целое число 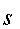 , то задачей
о рюкзаке является нахождение таких элементов
, то задачей
о рюкзаке является нахождение таких элементов 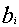 , сумма которых равна
, сумма которых равна 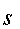 . Если в рюкзаке
лежит быстрорастущая последовательность чисел, то нет необходимости в полном
переборе элементов для того, чтобы найти нужный элемент. Для заданного
. Если в рюкзаке
лежит быстрорастущая последовательность чисел, то нет необходимости в полном
переборе элементов для того, чтобы найти нужный элемент. Для заданного 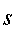 проверяем
проверяем 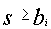 . Если ответ «нет», то
. Если ответ «нет», то 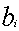 не может входить в сумму; в противном случае — должно входить. Это следует из
того, что оставшиеся элементы
не может входить в сумму; в противном случае — должно входить. Это следует из
того, что оставшиеся элементы 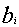 в сумме
дают число меньше
в сумме
дают число меньше 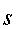 .
.
Входными
данными алгоритма кодировки с
использованием быстрорастущей
последовательности является множество
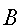 и целое число
и целое число
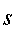 , для которого подбирается сумма элементов
, для которого подбирается сумма элементов
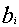 .
.
Выходными
данными является множество
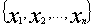 , где
, где
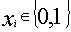 элементы такие, что
элементы такие, что
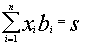 . Алгоритм построения следующий:
. Алгоритм построения следующий:
- i:=n
- while i
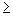 1 do
1 do
- 1 if
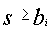 then
then 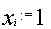 and
and 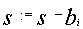 else
else 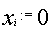
- 2
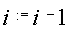
- 1 if
- Return (
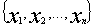 )
)
Каждый абонент, вступающий в переписку с использованием шифра, создает открытый ключ и соответствующий ему секретный. Алгоритм генерации ключей следующий:
- Фиксированное целое
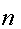 — параметр алгоритма.
— параметр алгоритма.
- Каждый абонент должен выполнить шаги 3-7.
- Выбирается быстрорастущая последовательность
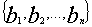 и модуль
и модуль 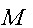 такой, что
такой, что 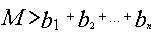
- Выбирается случайное целое
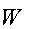 из интервала
из интервала
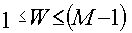 такое, что
такое, что 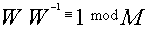 , где
, где 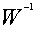 — число, обратное к
— число, обратное к 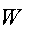 .
. - Выбирается случайная подстановка
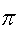 из целых чисел
из целых чисел 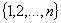 .
. - Вычисляются
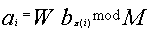 для всех <
для всех < 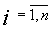 .
. - Открытым ключом является множество
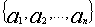 , а секретным ключом — совокупность
, а секретным ключом — совокупность 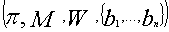 .
.
Теперь
если абонент В шифрует сообщение
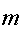 для абонента А,
который его расшифровывает, необходимо
выполнить следующую последовательность
действий:
для абонента А,
который его расшифровывает, необходимо
выполнить следующую последовательность
действий:
- Шифрование абонента В.
- Получить от А открытый ключ
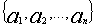 .
.
- Представить сообщение
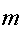 как бинарную
строку длиной
как бинарную
строку длиной 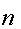 ,
, 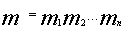 .
. - Вычислить целое
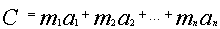 .
. - Отправить
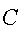 к А.
к А.
- Получить от А открытый ключ
- Расшифровка абонентом А.
- Получить сообщение
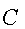 от В.
от В. - Вычислить
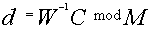 .
. - Используя алгоритм кодировки, найти целое
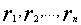 , где
, где 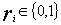 и удовлетворяет условию
и удовлетворяет условию 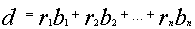 .
. - Открытый текст получается по подстановке
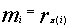 для
для 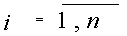 .
.
- Получить сообщение
Если у
абонента А n=6,
быстрорастущая последовательность (12, 17, 33,
74, 157, 316), M=737, W=635,
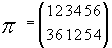 и открытый ключ (319,
196, 250, 477, 200, 559), при этом секретным ключом
является (
и открытый ключ (319,
196, 250, 477, 200, 559), при этом секретным ключом
является (
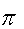 , М, W, (12, 17, 33,
74, 157, 316)). Открытый текст m=101101
обрабатывается на стороне абонента В <
, М, W, (12, 17, 33,
74, 157, 316)). Открытый текст m=101101
обрабатывается на стороне абонента В <
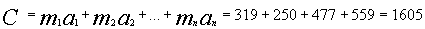 и посылается А. А
вычисляет
и посылается А. А
вычисляет
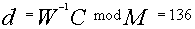 и
и
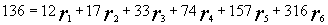 , что дает 136=12+17+33+74. Следовательно,
, что дает 136=12+17+33+74. Следовательно,
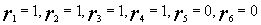 и после применения
подстановки
и после применения
подстановки
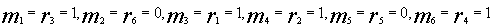 получаем исходный
открытый текст.
получаем исходный
открытый текст.
Если ОТ является слово «SAUNA», то для того, чтобы воспользоваться рюкзачным шифром, необходимо: разбить текст, например на биграммы {«SA», «UN», «A_» }, дополнив недостающую биграмму знаком раздела, и закодировать каждую биграмму. В результате может получиться битовая последовательность {100110001, 1010101110, 0000100000}, которую затем можно порциями обработать по алгоритму рассмотренного шифра.
Необходимо отметить, что в последнее время в информационной индустрии широкое распространение получили сетевые протоколы, поддерживающие секретные каналы передачи данных, такие как SSL, Open SSL, SSH и др.
SSL — Secure Sockets Layer (секретный уровень сокетов). Задача протокола SSL состоит в том, чтобы обеспечить секретность и надежность связи между двумя программными приложениями. Протокол состоит из двух уровней. На нижнем уровне многоуровневого транспортного протокола (например, TCP) SSL является протоколом записи. SSL используется для формирования пакета (инкапсуляции) различных протоколов более высокого уровня. Для каждого инкапсулированного протокола SSL позволяет серверу и клиенту подтверждать подлинность друг друга, выполнять алгоритмы шифрования и обмен криптографическими ключами прежде, чем протокол прикладной программы начнет передавать или получать данные. Преимущество SSL состоит в том, что он является независимым протоколом прикладной программы. Протокол более высокого уровня может лежать на уровень выше SSL.
Протокол SSL обеспечивает защиту связи, которая имеет три основные функции: обеспечение конфиденциального соединения за счет шифрования данных, например по алгоритму DES; шифрование с открытым ключом, используемое для подтверждения подлинности передатчика и получателя; поддержка надежности передачи данных за счет использования корректирующих кодов и безопасных хеш-функций.
В сочетании с протоколом HTTP и аутентификацией сервера протокол SSL обеспечивает необходимые функции шифрования и далее поддерживает установленное соединение, перепроверяя подлинность Web-сервера и т.п. Важно понять, что SSL только защищает связь в процессе передачи данных и не заменяет других защитных механизмов. Обратите внимание, что протокол инкапсулирует в себя алгоритмы шифрования, рассмотренные ранее.
Хорошая криптографическая система — это система, удерживающая равновесие между тем, что возможно, и тем, что приемлемо. Сильная криптография может противостоять целенаправленным атакам до некоторой точки — точки, в которой становится легче получить нужную информацию каким-то другим способом. Невозможно помешать злоумышленнику копаться в чужом мусоре. Но шифрование позволяет лишить его информации, например, о том, чей это мусор.
Желая защитить информацию и применяя какой-то криптографический продукт или разрабатывая собственную криптографическую систему из готовых компонентов, важно понимать механизм ее функционирования и присущие ей ограничения, хотя бы поверхностно. Надеемся, что данная публикация поможет вам в этом.








