Технологии коммутации
Коммутационные полносвязные матрицы
Баньяновидные коммутаторы (Banyan switch)
Коммутаторы Бенеша (Benes switch)
Те, кто хотя бы немного знаком с сетевыми технологиями, прекрасно знают, что основными устройствами для построения современных локальных и глобальных сетей являются коммутаторы. Как класс сетевых устройств коммутаторы развивались по мере развития самих сетей, и одновременно менялись и сами технологии коммутации, и архитектура коммутаторов.
ехнология
коммутации зародилась задолго до появления первого персонального компьютера
и первоначально была связана с телефонными сетями. Помните фильмы, в которых
телефонные барышни на коммутаторах вручную переключают штекеры на коммутационной
панели, обеспечивая тем самым коммутацию соединений телефонных линий? Конечно,
сегодняшние коммутаторы даже отдаленно не напоминают те раритетные телефонные
коммутационные панели, хотя и выполняют схожие задачи, причем архитектура современных
коммутаторов во многом основана на том математическом аппарате, который был
разработан еще в 50-х годах прошлого века.
Безусловно, особенности архитектуры коммутаторов во многом определяются сетевой технологией, но принципы построения остаются общими. В этой статье мы расскажем об основных технологиях, используемых в современных коммутаторах безотносительно к типу сетей, в которых эти коммутаторы применяются, тем более что используемые технологии находят применение и в сетях с коммутацией соединений, и в сетях с коммутацией пакетов. Поэтому в дальнейшем мы не будем концентрироваться на коммутаторах ATM, SONET или Ethernet, а сосредоточимся на базовых принципах самого коммутационного процесса.
Итак, в общем виде любой коммутатор представляет собой многопортовое устройство, содержащее N входных и N выходных портов (рис. 1). Вообще говоря, коммутаторы выполняют довольно широкий набор функций, но мы сосредоточим наше внимание только на процессе маршрутизации, то есть на пересылке пакетов от входного порта на выходной (его адрес обычно указывается в заголовке пакета).
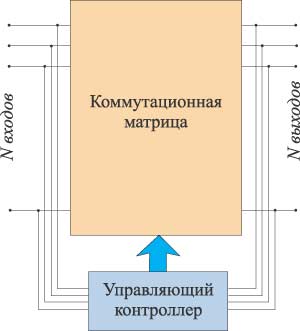
Рис. 1. Структурная схема коммутационной матрицы
Коммутационные полносвязные матрицы
оммутационные
полносвязные матрицы (crossbar switch) — наиболее простой для понимания тип
архитектуры. Фактически, здесь речь идет о матрице, линии которой образованы
проводниками, связанными с входами коммутатора, а столбцы — с выходами (рис.
2). На пересечении линий и столбцов матрицы находятся управляемые переключатели,
которые могут либо замыкать соединение линии на столбец, либо, наоборот, размыкать
его. В принципе, такая матричная архитектура напоминает самые первые телефонные
коммутаторы, где с помощью штекеров входные линии замыкались на выходные, образуя
соединение. Смысл, который вкладывается в понятие полносвязной архитектуры,
в данном случае заключается в том, что любой входной порт может быть связан
с любым выходным портом.
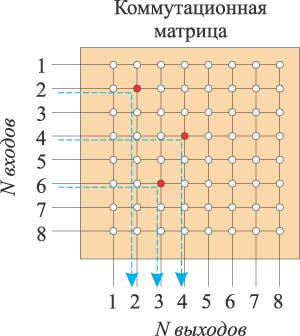
Рис. 2. Структура полносвязной коммутационной матрицы
Для управления переключателями, находящимися на пересечении линий и столбцов такой коммутационной матрицы, коммутатор должен иметь определенный контроллер, который управляет состоянием переключателей на основе анализа информации об адресе назначения. Указанные коммутационные архитектуры могут использоваться как в коммутаторах, ориентированных на коммутацию пакетов, так и на коммутацию соединений, и пригодны для применения в синхронных и асинхронных приложениях.
В рассмотренной нами коммутационной матрице N x N количество точек пересечения (crosspoints) линий и столбцов составляет N2, однако количество входов совсем необязательно должно совпадать с количеством выходов, то есть могут существовать коммутационные матрицы NxM — N входов и M выходов. С ростом числа входов и выходов усложняется и схемотехника коммутационной матрицы (в особенности управляющего контроллера), поэтому такие матрицы плохо масштабируются. При построении многопортовых коммутационных матриц используется несколько иной подход, который заключается в том, что простые коммутационные матрицы связываются между собой, образуя одну большую коммутационную матрицу.
Рассмотрим в качестве примера составную коммутационную матрицу 9x9, в которую входит шесть матриц 3x3 (рис. 3). В сравнении с коммутационной матрицей 9x9, имеющей 81 точку пересечения, составная матрица имеет только 54 точки пересечения и соответственно более простую схемотехнику. Однако если рассмотренные ранее полносвязные матрицы обеспечивали соединение любого входного порта с любым выходным, то в случае составной матрицы все оказывается не так просто. Предположим, что второй порт закоммутирован на пятый (соединение выделено на рис. 3 красным цветом), — в этом случае установить соединение между первым и четвертым или первым и шестым портами, равно как и между третьим и четвертым или третьим и шестым портами, оказывается невозможно. Фактически, следствием упрощения архитектуры матрицы является блокирование возможности устанавливать соединение между любыми парами портов, поэтому такая архитектура коммутационной матрицы получила название блокирующей. Если же архитектура обеспечивает возможность установления связи между любыми парами входных и выходных портов, то говорят о неблокирующей архитектуре коммутатора.
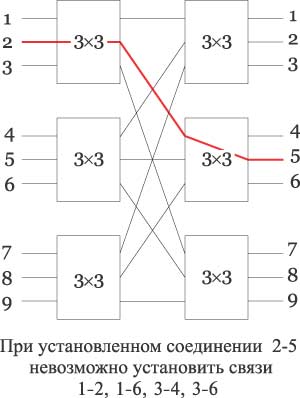
Рис. 3. Пример двухуровневой составной коммутационной матрицы
Чтобы избежать блокирования в составной коммутационной матрице, можно попытаться увеличить общее количество точек пересечения, добавив дополнительные коммутационные матрицы 3x3. На рис. 4 представлен пример составной трехкаскадной коммутационной матрицы, образованной девятью матрицами 3x3. Понятно, что суммарное количество точек пересечения здесь равно 81, однако в данном случае возможно установить соединение между первым и четвертым или первым и шестым портами, как и между третьим и четвертым или третьим и шестым портами, при установленном соединении между вторым и пятым портами. Впрочем, такой трехкаскадный коммутатор все же не является неблокирующим — пример блокировки соединения в таком коммутаторе показан на рис. 5.
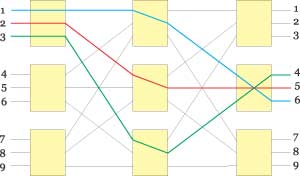
Рис. 4. Пример составного трехкаскадного коммутатора
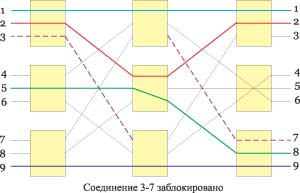
Рис. 4. Пример составного трехкаскадного коммутатора
В общем случае составная коммутационная матрица может состоять из более простых коммутаторов с неравным количеством входов и выходов. Рассмотрим в качестве примера составной трехкаскадный коммутатор, размер которого N x N (рис. 6). Если первый и последний каскады такого коммутатора образованы коммутаторами с n входами и k выходами, то их количество должно быть равно N/n в каждом уровне. Кроме того, в промежуточном каскаде должно быть ровно k коммутаторов с размерностью N/n Ѕ N/n, а количество точек пересечения, определяющее сложность составной схемы, составляет:
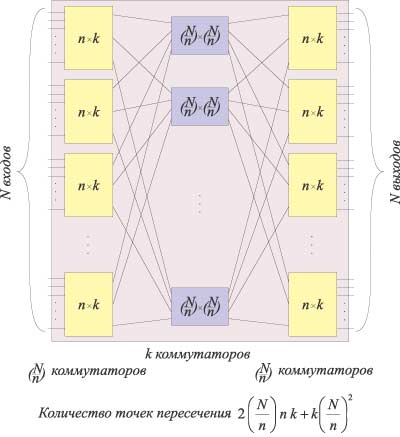
Рис. 6. Пример схемы составного коммутатора с размерностью NЅN
 |
|
Clos-коммутаторы
стественно
возникает вопрос: при какой архитектуре можно добиться минимального количества
точек пересечения и в то же время обеспечить неблокируемость?
Впервые вопрос о неблокирующей архитектуре составных коммутаторов был изучен Клосом (Clos) в 1950 году, то есть задолго до появления первого персонального компьютера, а коммутаторы с неблокирующей архитектурой стали называть в его честь Clos-коммутаторами. Клос доказал, что для того, чтобы трехкаскадный коммутатор имел неблокирующую архитектуру, необходимое количество коммутаторов k в среднем каскаде должно быть не меньше 2n–1.
Для доказательства условия Клоса рассмотрим трехкаскадный Clos-коммутатор (N, n, k), имеющий N входов, с размерностью коммутаторов в первом каскаде n x k, показанный на рис. 7. В самом худшем случае требуется установить соединение, исходящее от коммутатора n x k, в котором уже занято (n–1) соединений, оккупирующих (n–1) промежуточных коммутаторов, то есть коммутаторов второго каскада. Пусть, кроме того, это соединение требуется установить с выходным коммутатором, в котором также занято (n–1) выходов, которые занимают еще (n–1) коммутаторов второго каскада. Следовательно, занятыми оказываются 2(n–1) коммутаторов второго каскада, а для того, чтобы можно было установить еще одно соединение, потребуется еще один коммутатор во втором каскаде. Таким образом, их общее количество во втором каскаде должно быть не менее 2(n–1)+1=2n–1.
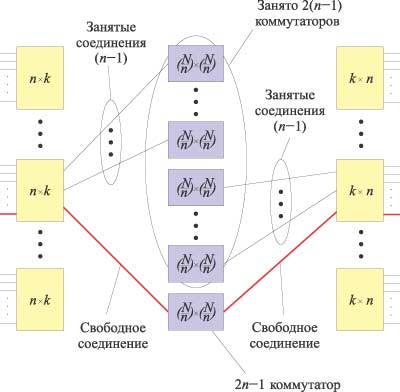
Рис. 7. Условие неблокирующей архитектуры трехкаскадного Clos-коммутатора (N, n, k)
Теперь рассмотрим, сколько точек пересечения имеет Clos-коммутатор (N, n, k). Учитывая, что количество коммутаторов во втором уровне должно быть равным k=2n–1, получим:
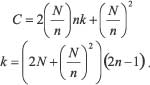
Как видите, количество точек пересечения зависит от размерности количества входов n в каждом коммутаторе первого каскада или от количества выходов в коммутаторах в третьем каскаде. Поэтому, продифференцировав данную зависимость по количеству входов n, можно определить минимальное количество точек пересечения:
Условие минимального значения определяется равенством нулю производной функции, но при достаточно большом значении n последним членом выражения можно пренебречь. Тогда:
Таким образом, для обеспечения минимально возможного количества точек пересечения необходимо, чтобы коммутаторы в первом уровне имели бы по N/2—входов и (2n–1) выходов.
Количество точек пересечения при этом будет равным:
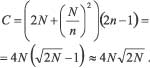
Как нетрудно заметить, полученное количество точек пересечения меньше, чем N2, при N>32.
Рассмотренная выше неблокирующая архитектура относится к типу строго неблокирующей архитектуры (strictly non-blocking). Существует и другой тип неблокирующей архитектуры, называемый перестраиваемой неблокирующей архитектурой. В данном случае подразумевается, что установить новое соединение между входом и выходом коммутатора возможно всегда, но при условии перестройки уже существующих соединений.
|
|
Баньяновидные коммутаторы (Banyan switch)
los-коммутаторы
— это не единственная архитектура, получившая распространение. Еще две интересные
архитектуры коммутационных матриц — это баньяновидные коммутаторы и коммутаторы
Бенеша.
В баньяновидных коммутаторах простейшим коммутационным элементом, называемым также бета-элементом (b-элемент), является коммутационная матрица, состоящая из двух входящих и двух выходящих портов.
Структурная схема такого базового элемента, представленная на рис. 8, включает управляющую логическую схему (decision logic), назначение которой заключается в обработке заголовков пакетов и в принятии решения о состоянии коммутационной матрицы, а также регистр-защелку (latch) для фиксации принятого решения и линий задержки (delay) в целях синхронизации коммутационной матрицы (Cross Connection) и входных сигналов. Сама коммутационная матрица может обеспечивать либо прямое соединение между входами и выходами, либо кроссоверное.
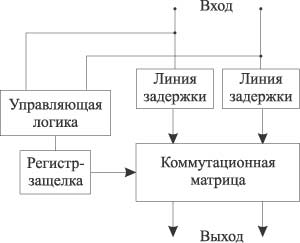
Рис. 8. Структурная схема базового коммутирующего элемента
Баньяновидные сети, похожие по форме на тропическое дерево баньян, строятся путем формирования рекурсивных каскадов бета-элементов, каждый из которых обрабатывает входящую ячейку в соответствии с управляющим битом выходного адреса. Если этот бит равен нулю, то коммутируется соединение с верхним выходным портом кросса, в противном случае — с нижним (рис. 9).
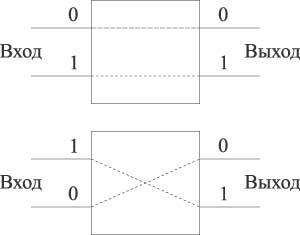
Рис. 9. Коммутация в бета-элементе в зависимости от значения управляющего бита
При построении баньяновидного коммутатора 4x4 используются два каскада бета-элементов, а для построения маршрута коммутации необходимо использовать уже два бита выходного адреса. Первый бит выходного адреса применяется для указания бета-элемента, на который направляется кадр, а второй — для указания порта бета-элемента второго каскада (рис. 10).
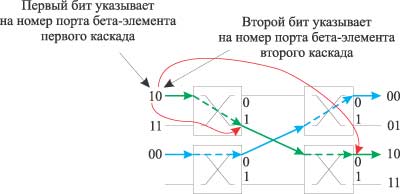
Рис. 10. Баньяновидный коммутационный элемент 4Ѕ4
Баньяновидный коммутационный элемент размером 8Ѕ8 формируется рекурсивно и состоит из трех каскадов бета-элементов, а для указания маршрута коммутации требуется использовать уже три адресных бита: первый бит применяется на номер порта коммутации бета-элемента первого каскада, второй — на номер порта коммутации бета-элемента второго каскада, а третий — на номер порта коммутации бета-элемента третьего каскада (рис. 11).
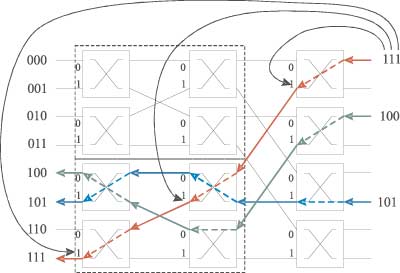
Рис. 11. Баньяновидный коммутационный элемент 8Ѕ8
Учитывая рекурсивный способ формирования каскадов баньяновидных коммутационных сетей, нетрудно подсчитать, что количество входов в таких коммутационных сетях представляется как степень числа 2 (2, 4, 8, 16, 32 и т.д.) и с увеличением числа входов вдвое добавляется еще один каскад, поэтому количество входов можно связать с числом каскадов по формуле N = 2k, где k — количество каскадов в схеме. Соответственно количество каскадов определяется как k = log2N, а учитывая то, что в каждом каскаде имеется N/2 бета-элементов, мы найдем, что в баньяновидной коммутационной сети размером NxN общее количество бета-элементов составит (N/2)log2N.
Популярность баньяновидных сетей объясняется использованием простых коммутационных элементов для обеспечения процесса коммутации, что позволяет при создании больших коммутаторов легко реализовать модульный рекурсивный подход на уровне аппаратных средств.
Минусом баньяновидных сетей является их блокирующая архитектура, причем вероятность блокировки быстро возрастает с ростом сети. Пример возникновения блокировки в баньяновидной сети показан на рис. 12.
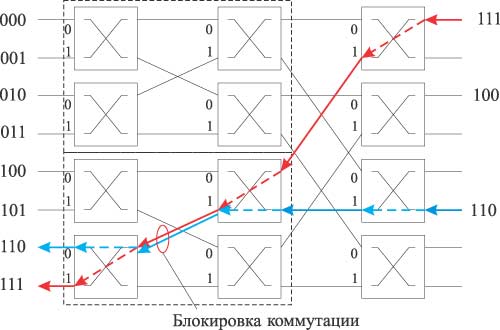
Рис. 12. Возникновение блокировки коммутации в баньяновидной сети 8Ѕ8
В общем случае можно доказать, что при построении многокаскадных коммутируемых сетей с неблокирующей архитектурой минимальное число бета-элементов должно быть равным Nlog2N, вследствие чего баньяновидные сети не имеют неблокирующей архитектуры. Одно из возможных решений проблемы блокировки в баньяновидных сетях состоит в добавлении специального сортировщика Бэтчера, который позволяет избежать блокировок при адресации соединений на различные выходные порты. Отметим также, что баньяновидные коммутаторы называют самомаршрутизирующимися (self-routing) — в том смысле, что состояние каждого бета-элемента определяется только информацией, содержащейся во входном пакете.
|
|
Коммутаторы Бенеша (Benes switch)
ще
один широко распространенный тип составных коммутационных сетей — коммутаторы
Бенеша (Benes). Эти сети также составляются из бета-элементов с общим количеством
Nlog2N и имеют неблокирующую перестраиваемую архитектуру. Однако данные коммутаторы
не являются самомаршрутизирующими, то есть для коммутации маршрута недостаточно
информации, содержащейся во входном пакете, и для определения состояния всех
бета-элементов необходим контроллер.
Пример коммутатора Бенеша представлен на рис. 13.
Рис. 13. Коммутатор Бенеша при возникновении блокировки и после перестройки
***
Рассмотренные выше схемы коммутации не исчерпывают список схем, применяемых в современном сетевом оборудовании. Во многих случаях используются комбинационные схемы с применением технологии временного разделения (Time Division Multiplexing, TDM). Кроме того, немаловажное значение имеет и буферизация, позволяющая создавать неблокирующую архитектуру. Однако в данной статье мы не задавались целью описать во всех деталях архитектурные особенности коммутаторов, а представили лишь краткий обзор основных схем.
