Обзор программ для символьной математики
Символьная, или, как еще говорят, компьютерная, математика либо компьютерная алгебра, — большой раздел математического моделирования. В принципе, программы такого рода можно отнести к инженерным программам автоматизированного проектирования. Таким образом, в области инженерного проектирования выделяют три основных раздела:
- CAD — Computer Aided Design;
- CAM — Computer Aided Manufacturing;
- CAE — Computer Aided Engeneering.
Сегодня серьезное конструирование, градостроительство и архитектура, электротехника и масса смежных с ними отраслей, а также учебные заведения технической направленности уже не могут обойтись без систем автоматизированного проектирования (САПР), производства и расчетов. А математические пакеты являются составной частью мира CAE-систем, но эта часть никак не может считаться второстепенной, поскольку некоторые задачи вообще невозможно решить без помощи компьютера. Более того, к системам символьной математики сегодня прибегают даже теоретики (так называемые чистые, а не прикладные математики), например для проверки своих гипотез.
Всего каких-нибудь 10 лет назад эти системы считались сугубо профессиональными, но середина 90-х годов стала переломным моментом для мирового рынка CAD/CAM/CAE-систем массового применения. Тогда, впервые за долгое время, пакеты для параметрического моделирования с промышленными возможностями стали доступны пользователям персональных компьютеров. Создатели подобных систем учли требования широкого круга пользователей и таким образом дали возможность десяткам тысяч инженеров и математиков использовать на своих персональных рабочих местах новейшие достижения науки в области технологий CAD/CAM/CAE-систем.
Так что же умеют программы математического моделирования? Неужели они требуют от ученых умения программировать на тех или иных алгоритмических языках, отлаживать программы, отлавливать ошибки и тратить массу времени на получение результата? Нет, те времена давно прошли, и теперь в математических пакетах применяется принцип конструирования модели, а не традиционное «искусство программирования». То есть пользователь лишь ставит задачу, а методы и алгоритмы решения система находит сама. Более того, такие рутинные операции, как раскрывание скобок, преобразование выражений, нахождение корней уравнений, производных и неопределенных интегралов компьютер самостоятельно осуществляет в символьном виде, причем практически без вмешательства пользователя.
Современные математические пакеты можно использовать и как обычный калькулятор, и как средства для упрощения выражений при решении каких-либо задач, и как генератор графики или даже звука! Стандартными стали также средства взаимодействия с Интернетом, и генерация HTML-страниц выполняется теперь прямо в процессе вычислений. Теперь можно решать задачу и одновременно публиковать для коллег ход ее решения на своей домашней странице.
Рассказывать о программах математического моделирования и возможных областях их применения можно очень долго, но мы ограничимся лишь кратким обзором ведущих программ, укажем их общие черты и различия. В настоящее время практически все современные CAE-программы имеют встроенные функции символьных вычислений. Однако наиболее известными и приспособленными для математических символьных вычислений считаются Maple, MathCad, Mathematica и MatLab. Но, делая обзор основных программ символьной математики, мы укажем и на возможные альтернативы, идеологически схожие с тем или иным пакетом-лидером.
Так что же делают эти программы и как они помогают математикам? Основу курса математического анализа в высшей школе составляют такие понятия, как пределы, производные, первообразные функций, интегралы разных видов, ряды и дифференциальные уравнения. Тому, кто знаком с основами высшей математики, наверняка известны десятки правил нахождения пределов, взятия интегралов, нахождения производных и т.д. Если добавить к этому то, что для нахождения большинства интегралов нужно также помнить таблицу основных интегралов, то получается поистине огромный объем информации. И если какое-то время не тренироваться в решений подобных задач, то многое быстро забывается и для нахождения, например, интеграла посложнее придется уже заглядывать в справочники. Но ведь взятие интегралов и нахождение пределов в реальной работе не является главной целью вычислений. Реальная цель заключается в решении каких-либо проблем, а вычисления — всего лишь промежуточный этап на пути к этому решению.
С помощью описываемого ПО можно сэкономить массу времени и избежать многих ошибок при вычислениях. Естественно, CAE системы не ограничиваются только этими возможностями, но в данном обзоре мы сделаем упор именно на них.
Отметим только, что спектр задач, решаемых подобными системами, очень широк:
- проведение математических исследований, требующих вычислений и аналитических выкладок;
- разработка и анализ алгоритмов;
- математическое моделирование и компьютерный эксперимент;
- анализ и обработка данных;
- визуализация, научная и инженерная графика;
- разработка графических и расчетных приложений.
При этом отметим, что поскольку CAE-системы содержат операторы для базовых вычислений, то почти все алгоритмы, отсутствующие в стандартных функциях, можно реализовать посредством написания собственной программы.
Mathematica (http://www.wolfram.com/)
Минимальные требования к системе:
- процессор Pentium II или выше;
- 128 Мбайт оперативной памяти (рекомендуется 256 Мбайт или больше);
- 400-550 Мбайт дискового пространства;
- операционные системы: Windows 98/Me/ NT 4.0/2000/2003 Server/2003x64/XP/XP x64.
Компания Wolfram Reseach, Inc., разработавшая систему компьютерной математики Mathematica, по праву считается старейшим и наиболее солидным игроком в этой области. Пакет Mathematica (текущая версия 5.2) повсеместно применяется при расчетах в современных научных исследованиях и получил широкую известность в научной и образовательной среде. Можно даже сказать, что Mathematica обладает значительной функциональной избыточностью (там, в частности, есть даже возможность для синтеза звука).
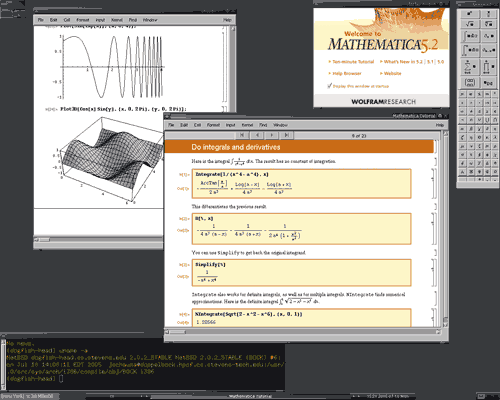
Однако вряд ли эта мощная математическая система, претендующая на мировое лидерство, нужна секретарше или даже директору небольшой коммерческой фирмы, не говоря уже о рядовых пользователях. Но, несомненно, любая серьезная научная лаборатория или кафедра вуза должна иметь подобную программу, если там всерьез заинтересованы в автоматизации выполнения математических расчетов любой степени сложности. Несмотря на свою направленность на серьезные математические вычисления, системы класса Mathematica просты в освоении и могут использоваться довольно широкой категорией пользователей — студентами и преподавателями вузов, инженерами, аспирантами, научными работниками и даже учащимся математических классов общеобразовательных и специальных школ. Все они найдут в подобной системе многочисленные полезные возможности для применения.
При этом широчайшие функции программы не перегружают ее интерфейс и не замедляют вычислений. Mathematica неизменно демонстрирует высокую скорость символьных преобразований и численных расчетов. Программа Mathematica из всех рассматриваемых систем наиболее полна и универсальна, однако у каждой программы есть как свои достоинства, так и недостатки. А главное — у них есть свои приверженцы, которых бесполезно убеждать в превосходстве другой системы. Но те, кто серьезно работает с системами компьютерной математики, должны пользоваться несколькими программами, ибо только это гарантирует высокий уровень надежности сложных вычислений.
Отметим, что в разработках различных версий системы Mathematica, наряду с головной фирмой Wolfram Research, Inc., принимали участие другие фирмы и сотни специалистов высокой квалификации, в том числе математики и программисты. Есть среди них и представители пользующейся уважением и спросом за рубежом математической школы России. Система Mathematica является одной из самых крупных программных систем и реализует наиболее эффективные алгоритмы вычислений. К их числу, например, относится механизм контекстов, исключающий появление в программах побочных эффектов.
Система Mathematica сегодня рассматривается как мировой лидер среди компьютерных систем символьной математики для ПК, обеспечивающих не только возможности выполнения сложных численных расчетов с выводом их результатов в самом изысканном графическом виде, но и проведение особо трудоемких аналитических преобразований и вычислений. Версии системы под Windows имеют современный пользовательский интерфейс и позволяют готовить документы в форме Notebooks (записных книжек). Они объединяют исходные данные, описания алгоритмов решения задач, программ и результатов решения в самой разнообразной форме (математические формулы, числа, векторы, матрицы, таблицы и графики).
Mathematica была задумана как система, максимально автоматизирующая труд научных работников и математиков-аналитиков, поэтому она заслуживает изучения даже в качестве типичного представителя элитных и высокоинтеллектуальных программных продуктов высшей степени сложности. Однако куда больший интерес она представляет как мощный и гибкий математический инструментарий, который может оказать неоценимую помощь большинству научных работников, преподавателей университетов и вузов, студентов, инженеров и даже школьников.
С самого начала большое внимание уделялось графике, в том числе динамической, и даже возможностям мультимедиа — воспроизведению динамической анимации и синтезу звуков. Набор функций графики и изменяющих их действие опций очень широк. Графика всегда была сильной стороной различных версий системы Mathematica и обеспечивала им лидерство среди систем компьютерной математики.
В результате Mathematica быстро заняла ведущие позиции на рынке символьных математических систем. Особенно привлекательны обширные графические возможности системы и реализация интерфейса типа Notebook. При этом система обеспечивала динамическую связь между ячейками документов в стиле электронных таблиц даже при решении символьных задач, что принципиально и выгодно отличало ее от других подобных систем.
Кстати, центральное место в системах класса Mathematica занимает машинно-независимое ядро математических операций, которое позволяет переносить систему на различные компьютерные платформы. Для переноса системы на другую компьютерную платформу используется программный интерфейсный процессор Front End. Именно он определяет, какой вид имеет пользовательский интерфейс системы, то есть интерфейсные процессоры систем Mathematica для других платформ могут обладать своими нюансами. Ядро сделано достаточно компактным для того, чтобы можно было очень быстро вызвать из него любую функцию. Для расширения набора функций служат библиотека (Library) и набор пакетов расширения (Add-on Packages). Пакеты расширений готовятся на собственном языке программирования систем Mathematica и являются главным средством для развития возможностей системы и их адаптации к решению конкретных классов задач пользователя. Кроме того, системы имеют встроенную электронную справочную систему — Help, которая содержит электронные книги с реальными примерами.
Таким образом, Mathematica — это, с одной стороны, типичная система программирования на базе одного из самых мощных проблемноориентированных языков функционального программирования высокого уровня, предназначенная для решения различных задач (в том числе и математических), а с другой — интерактивная система для решения большинства математических задач в диалоговом режиме без традиционного программирования. Таким образом, Mathematica как система программирования имеет все возможности для разработки и создания практически любых управляющих структур, организации ввода-вывода, работы с системными функциями и обслуживания любых периферийных устройств, а с помощью пакетов расширения (Add-ons) появляется возможность подстраиваться под запросы любого пользователя, (хотя рядовому пользователю эти средства программирования могут и не понадобиться — он вполне обойдется встроенными математическими функциями системы, поражающими своим обилием и многообразием даже опытных математиков).
К недостаткам системы Mathematica следует отнести разве что весьма необычный язык программирования, обращение к которому, впрочем, облегчает подробная система помощи.
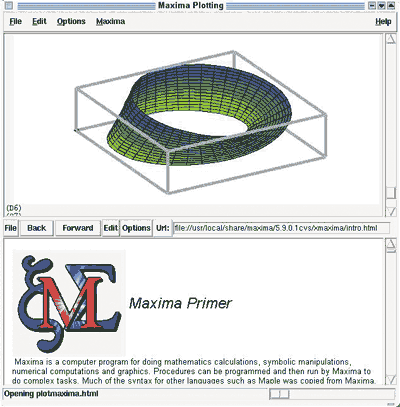
В качестве более простых, но идеологически близких альтернатив программы Mathematica можно назвать такие пакеты, как Maxima (http://maxima.sourceforge.net/) и Kalamaris (developer.kde.org/~larrosa/kalamaris.html).
Отметим, что система Maxima — это некоммерческий проект с открытым кодом. В программе Maxima для математической работы используется язык, сходный с языком в пакете Mathematica, а графический интерфейс построен по тем же принципам. Изначально программа называлась Xmaxima и создавалась для UNIX-систем.
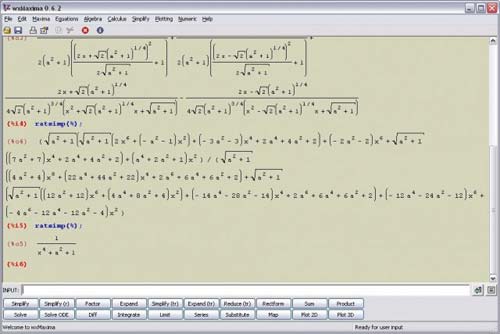
Кроме того, сейчас у системы Maxima есть еще более мощный, эффективный и дружественный кроссплатформенный графический интерфейс, который называется Wxmaxima (http://wxmaxima.sourceforge.net). И хотя этот проект пока что существует лишь в бета-версии, он постепенно превращается в очень серьезную альтернативу коммерческим системам.
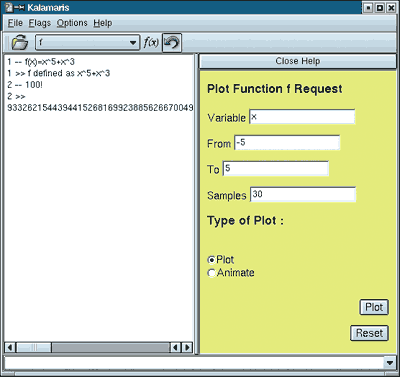
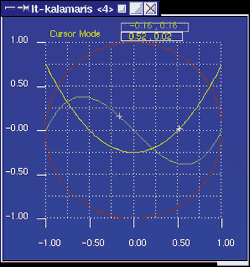
Что касается программы Kalamaris, то это также новый проект, который имеет подход и идеологию, схожие с системой Mathematica. Проект еще не завершен, но тоже является неплохой бесплатной альтернативой такому коммерческому монстру, как Mathematica.
Maple (http://www.maplesoft.com/)
Минимальные требования к системе:
• процессор Pentium III 650 МГц;
• 128 Мбайт оперативной памяти (рекомендуется 256 Мбайт);
• 400 Мбайт дискового пространства;
• операционные системы: Windows NT 4 (SP5)/98/ME/2000/2003 Server/XP Pro/XP Home.
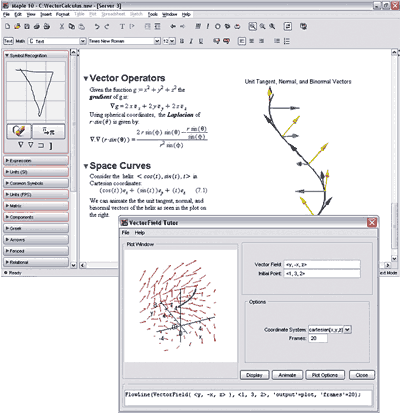
Программа Maple (последняя версия 10.02) — своего рода патриарх в семействе систем символьной математики и до сих пор является одним из лидеров среди универсальных систем символьных вычислений. Она предоставляет пользователю удобную интеллектуальную среду для математических исследований любого уровня и пользуется особой популярностью в научной среде. Отметим, что символьный анализатор программы Maple является наиболее сильной частью этого ПО, поэтому именно он был позаимствован и включен в ряд других CAE-пакетов, таких как MathCad и MatLab, а также в состав пакетов для подготовки научных публикаций Scientific WorkPlace и Math Office for Word.
Пакет Maple — совместная разработка Университета Ватерлоо (шт. Онтарио, Канада) и Высшей технической школы (ETHZ, Цюрих, Швейцария). Для его продажи была создана специальная компания — Waterloo Maple, Inc., которая, к сожалению, больше прославилась математической проработкой своего проекта, чем уровнем его коммерческой реализации. В результате система Maple ранее была доступна преимущественно узкому кругу профессионалов. Сейчас эта компания работает совместно с более преуспевающей в коммерции и в проработке пользовательского интерфейса математических систем фирмой MathSoft, Inc. — создательницей весьма популярных и массовых систем для численных расчетов MathCad, ставших международным стандартом для технических вычислений.
Maple предоставляет удобную среду для компьютерных экспериментов, в ходе которых пробуются различные подходы к задаче, анализируются частные решения, а при необходимости программирования отбираются требующие особой скорости фрагменты. Пакет позволяет создавать интегрированные среды с участием других систем и универсальных языков программирования высокого уровня. Когда расчеты произведены и требуется оформить результаты, то можно использовать средства этого пакета для визуализации данных и подготовки иллюстраций для публикации. Для завершения работы остается подготовить печатный материал (отчет, статью, книгу) прямо в среде Maple, а затем можно приступать к очередному исследованию. Работа проходит интерактивно — пользователь вводит команды и тут же видит на экране результат их выполнения. При этом пакет Maple совсем не похож на традиционную среду программирования, где требуется жесткая формализация всех переменных и действий с ними. Здесь же автоматически обеспечивается выбор подходящих типов переменных и проверяется корректность выполнения операций, так что в общем случае не требуется описания переменных и строгой формализации записи.
Пакет Maple состоит из ядра (процедур, написанных на языке С и хорошо оптимизированных), библиотеки, написанной на Maple-языке, и развитого внешнего интерфейса. Ядро выполняет большинство базовых операций, а библиотека содержит множество команд — процедур, выполняемых в режиме интерпретации.
Интерфейс Maple основан на концепции рабочего поля (worksheet) или документа, содержащего строки ввода-вывода и текст, а также графику.
Работа с пакетом происходит в режиме интерпретатора. В строке ввода пользователь задает команду, нажимает клавишу Enter и получает результат — строку (или строки) вывода либо сообщение об ошибочно введенной команде. Тут же выдается приглашение вводить новую команду и т.д.
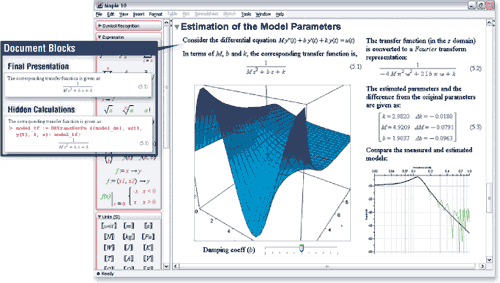
Интерфейс Maple
Рабочие окна (листы) системы Maple могут быть использованы либо как интерактивные среды для решения задач, либо как система для подготовки технической документации. Исполнительные группы и электронные таблицы упрощают взаимодействие пользователя с движком Maple, выполняя роль тех первичных средств, при помощи которых в систему Maple передаются запросы на выполнение конкретных задач и вывод результатов. Оба эти типа первичных средств допускают возможность ввода команд Maple.
Система Maple позволяет вводить электронные таблицы, содержащие как числа, так и символы. Они совмещают в себе математические возможности системы Maple с уже знакомым форматом из строк и столбцов традиционных электронных таблиц. Электронные таблицы системы Maple можно использовать для создания таблиц формул.
Для облегчения документирования и организации результатов вычислений имеются опции разбиения на параграфы и разделы, а также добавления гиперссылок. Гиперссылка является навигационным средством. Одним щелчком мыши по ней вы можете перейти к другой точке в пределах рабочего листа, к другому рабочему листу, к странице помощи, к рабочему листу на Web-сервере или к любой другой Web-странице.
Рабочие листы можно организовать иерархически, в виде разделов и подразделов. Разделы и подразделы можно как расширять, так и сворачивать. Система Maple, подобно другим текстовым редакторам, поддерживает опцию закладок.
Вычисления в Maple
Систему Maple можно использовать и на самом элементарном уровне ее возможностей — как очень мощный калькулятор для вычислений по заданным формулам, но главным ее достоинством является способность выполнять арифметические действия в символьном виде, то есть так, как это делает человек. При работе с дробями и корнями программа не приводит их в процессе вычислений к десятичному виду, а производит необходимые сокращения и преобразования в столбик, что позволяет избежать ошибок при округлении. Для работы с десятичными эквивалентами в системе Maple имеется специальная команда, аппроксимирующая значение выражения в формате чисел с плавающей запятой. Система Maple вычисляет конечные и бесконечные суммы и произведения, выполняет вычислительные операции с комплексными числами, легко приводит комплексное число к числу в полярных координатах, вычисляет числовые значения элементарных функций, а также знает много специальных функций и математических констант (таких, например, как «е» и «пи»). Maple поддерживает сотни специальных функций и чисел, встречающихся во многих областях математики, науки и техники. Приведем лишь некоторые из них:
- функция ошибок;
- эйлерова константа;
- экспоненциальный интеграл;
- эллиптическая интегральная функция;
- гамма-функция;
- зета-функция;
- ступенчатая функция Хевисайда;
- дельта-функция Дирака;
- бесселева и модифицированная бесселева функции.
Система Maple предлагает различные способы представления, сокращения и преобразования выражений, например такие операции, как упрощение и разложение на множители алгебраических выражений и приведение их к различному виду. Таким образом, Maple можно использовать для решения уравнений и систем.
Maple также имеет множество мощных инструментальных средств для вычисления выражений с одной или несколькими переменными. Программу можно использовать для решения задач дифференциального и интегрального исчисления, вычисления пределов, разложений в ряды, суммирования рядов, умножения, интегральных преобразований (таких как преобразование Лапласа, Z-преобразование, преобразование Меллина или Фурье), а также для исследования непрерывных или кусочно-непрерывных функций.
Maple может вычислять пределы функций, как конечные, так и стремящиеся к бесконечности, а также распознает неопределенности в пределах. В этой системе можно решать множество обычных дифференциальных уравнений (ODE), а также дифференциальные уравнения в частных производных (PDE), в том числе задачи с начальными условиями (IVP) и задачи с граничными условиями (BVP).
Одним из наиболее часто используемых в системе Maple пакетов программ является пакет линейной алгебры, содержащий мощный набор команд для работы с векторами и матрицами. Maple может находить собственные значения и собственные векторы операторов, вычислять криволинейные координаты, находить матричные нормы и вычислять множество различных типов разложения матриц.
Для технических применений в Maple включены справочники физических констант и единицы физических величин с автоматическим пересчетом формул. Особенно эффективна Maple при обучении математике. Высочайший интеллект этой системы символьной математики сочетается с прекрасными средствами математического численного моделирования и с просто потрясающими возможностями графической визуализации решений. Такие системы, как Maple, можно применять как в преподавании, так и для самообразования при изучении математики от самых азов до вершин.
Графика в Maple
Система Maple поддерживает как двумерную, так и трехмерную графику. Таким образом, можно представить явные, неявные и параметрические функции, а также многомерные функции и просто наборы данных в графическом виде и визуально искать закономерности.
Графические средства Maple позволяют строить двумерные графики сразу нескольких функций, создавать графики конформных преобразований функций с комплексными числами и строить графики функций в логарифмической, двойной логарифмической, параметрической, фазовой, полярной и контурной форме. Можно графически представлять неравенства, неявно заданные функции, решения дифференциальных уравнений и корневые годографы.
Maple может строить поверхности и кривые в трехмерном представлении, включая поверхности, заданные явной и параметрической функциями, а также решениями дифференциальных уравнений. При этом представлять можно не только в статическом виде, но и в виде двух- или трехмерной анимации. Эту особенность системы можно использовать для отображения процессов, протекающих в режиме реального времени.
Отметим, что для подготовки результата и документирования исследований в системе имеются все возможности выбора шрифтов для названий, надписей и другой текстовой информации на графиках. При этом можно варьировать не только шрифты, но и яркость, цвет и масштаб графика.
Специализированные приложения
Обширный набор мощных инструментальных приложений Maple PowerTools и пакетов для таких областей, как анализ методом конечных элементов (FEM), нелинейная оптимизация и др., полностью удовлетворят пользователей с университетским математическим образованием. В Maple включены также пакеты подпрограмм для решения задач линейной и тензорной алгебры, евклидовой и аналитической геометрии, теории чисел, теории вероятностей и математической статистики, комбинаторики, теории групп, интегральных преобразований, численной аппроксимации и линейной оптимизации (симплекс-метод), а также задач финансовой математики и многих, многих других.
Для финансовых расчетов предназначен программный пакет Finance. C его помощью можно вычислять текущую и накопленную сумму ежегодной ренты, совокупную ежегодную ренту, сумму пожизненной ренты, совокупную пожизненную ренту и процентный доход на облигации. Вы можете строить таблицу амортизации, определять реальную сумму ставки для сложных процентов и вычислять текущее и будущее фиксированное количество для конкретной ставки и сложных процентов.
Программирование
Система Maple использует процедурный язык 4-го поколения (4GL). Этот язык специально предназначен для быстрой разработки математических подпрограмм и пользовательских приложений. Синтаксис данного языка аналогичен синтаксису универсальных языков высокого уровня: C, Fortran, Basic и Pascal.
Maple может генерировать код, совместимый с такими языками программирования, как Fortran или C, и с языком набора текста LaTeX, который пользуется большой популярностью в научном мире и применяется для оформления публикаций. Одно из преимуществ этого свойства — способность обеспечивать доступ к специализированным числовым программам, максимально ускоряющим решение сложных задач. Например, используя систему Maple, можно разработать определенную математическую модель, а затем с ее помощью сгенерировать код на языке C, соответствующий этой модели. Язык 4GL, специально оптимизированный для разработки математических приложений, позволяет сократить процесс разработки, а настроить пользовательский интерфейс помогают элементы Maplets или документы Maple со встроенными графическими компонентами.
Одновременно в среде Maple можно подготовить и документацию к приложению, так как средства пакета позволяют создавать технические документы профессионального вида, содержащие текст, интерактивные математические вычисления, графики, рисунки и даже звук. Вы также можете создавать интерактивные документы и презентации, добавляя кнопки, бегунки и другие компоненты, и, наконец, публиковать документы в Интернете и развертывать интерактивные вычисления в Сети, используя сервер MapleNet.
Интернет-совместимость
Maple является первым универсальным математическим пакетом, который предлагает полную поддержку стандарта MathML 2.0, управляющего как внешним видом, так и смыслом математики в Интернете. Эта эксклюзивная функция делает текущую версию MathML основным средством Интернет-математики, а также устанавливает новый уровень совместимости многопользовательской среды. TCP/IP-протокол обеспечивает динамический доступ к информации из других Интернет-ресурсов, например к данным для финансового анализа в реальном времени или к данным о погоде.
Перспективы развития
Последние версии Maple, помимо дополнительных алгоритмов и методов решения математических задач, получили более удобный графический интерфейс, продвинутые инструменты визуализации и построения графиков, а также дополнительные средства программирования (в том числе по совместимости с универсальными языками программирования). Начиная с девятой версии в пакет был добавлен импорт документов из программы Mathematica, а в справочную систему были введены определения математических и инженерных понятий и расширена навигация по страницам справки. Кроме того, было повышено полиграфическое качество формул, особенно при форматировании больших и сложных выражений, а также значительно сокращен размер MW-файлов для хранения рабочих документов Maple.
Таким образом, Maple — это, пожалуй, наиболее удачно сбалансированная система и бесспорный лидер по возможностям символьных вычислений для математики. При этом оригинальный символьный движок сочетается здесь с легко запоминающимся структурным языком программирования, так что Maple может быть использована как для небольших задач, так и для серьезных проектов.
К недостаткам системы Maple можно отнести лишь ее некоторую «задумчивость», причем не всегда обоснованную, а также очень высокую стоимость этой программы (в зависимости от версии и набора библиотек цена ее доходит до нескольких десятков тысяч долл., правда студентам и научным работникам предлагаются дешевые версии — за несколько сотен долл.).
Пакет Maple широко распространен в университетах ведущих научных держав, в исследовательских центрах и компаниях. Программа постоянно развивается, вбирая в себя новые разделы математики, приобретая новые функции и обеспечивая лучшую среду для исследовательской работы. Одно из основных направлений развития этой системы — повышение мощности и достоверности аналитических (символьных) вычислений. Это направление представлено в Maple наиболее широко. Уже сегодня Maple может выполнять сложнейшие аналитические вычисления, которые нередко не по силам даже опытным математикам. Конечно же, Maple не способна на гениальные догадки, но зато рутинные и массовые расчеты система выполняет с блеском. Другое важное направление — повышение эффективности численных расчетов. В результате этого заметно возросла перспектива использования Maple в численном моделировании и в выполнении сложных вычислений — в том числе с произвольной точностью. И наконец, тесная интеграция Maple с другими программными средствами — еще одно важное направление развития этой системы. Ядро символьных вычислений Maple уже включено в состав целого ряда систем компьютерной математики — от систем для широкого круга пользователей типа MathCad до одной из лучших систем для численных расчетов и моделирования MatLab.
Все эти возможности в сочетании с прекрасно выполненным и удобным пользовательским интерфейсом и мощной справочной системой делают Maple первоклассной программной средой для решения самых разнообразных математических задач, способной оказать пользователям действенную помощь в решении учебных и реальных научно-технических задач.
Альтернативные пакеты
В качестве более простых, но идеологически близких альтернатив программе Maple можно отметить такие пакеты, как Derive (http://www.chartwellyorke.com/derive.html), Scientific WorkPlace (http://www.mackichan.com/) и YaCaS (www.xs4all.nl/~apinkus/yacas.html).
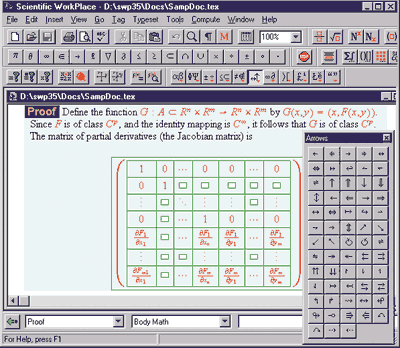
Как мы уже говорили, система Scientific WorkPlace (SWP, текущая версия 5.5) поначалу развивалась как редактор научных текстов, позволяя легко набирать и редактировать математические формулы. Однако со временем компания MacKichan Software, Inc. (разработчик системы Scientific WorkPlace) лицензировала символьный движок Maple у компании Waterloo Maple, Inc., и теперь эта программа объединяет простой в использовании текстовый процессор, обеспечивающий создание математических текстов и систему компьютерной алгебры в одной среде. Благодаря встроенной системе компьютерной алгебры вы можете производить вычисления прямо в документе. Конечно, у этой программы нет таких возможностей, как у Maple, однако она маленькая и простая в использовании.
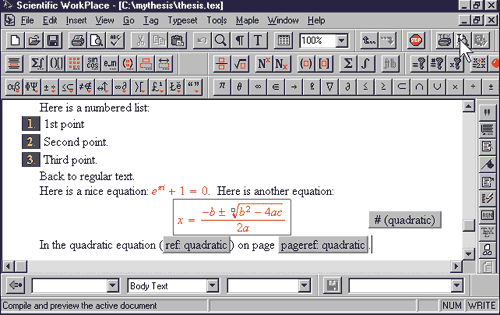
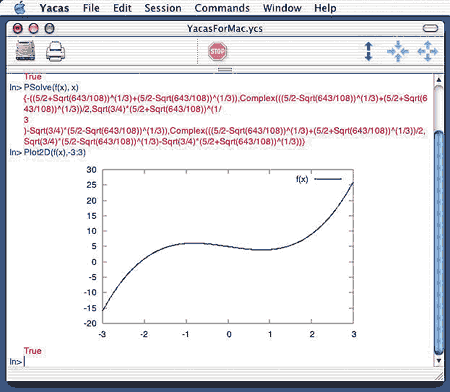
Что касается YaCaS (аббревиатура от выражения Yet Another Computer Algebra System — еще одна система компьютерной алгебры), то это бесплатная кроссплатформенная альтернатива Maple, построенная на тех же принципах. Мощный и высокоэффективный движок YaCaS полностью реализован на C++ на условиях открытой лицензии (OpenSource). Интерфейс, конечно, более бедный и простой, чем у маститых конкурентов, но довольно удобный.
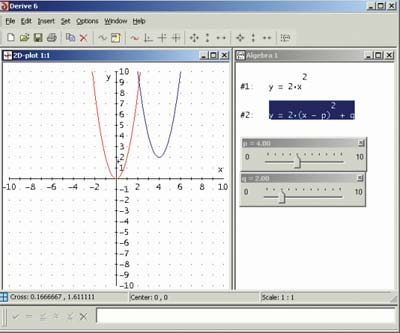
А вот маленькая коммерческая математическая система Derive (текущая версия 6.1) существует уже довольно давно, но, конечно, не может рассматриваться как полноценная альтернатива Maple, хотя она и по сей день привлекательна своей нетребовательностью к аппаратным ресурсам ПК. Более того, при решении задач умеренной сложности она демонстрирует даже более высокое быстродействие и большую надежность решения, чем первые версии систем Maple и Mathematica. Впрочем, системе Derive трудно всерьез конкурировать с этими системами — как по обилию функций и правил аналитических преобразований, так и по возможностям машинной графики и по удобству пользовательского интерфейса. Пока что Derive является больше учебной системой компьютерной алгебры начального уровня.
И хотя новейшая версия Derive 6 под Windows уже имеет современный удобный интерфейс, он во многом уступает изысканному интерфейсу маститых конкурентов. А в плане возможности графической визуализации результатов вычислений Derive и вообще далеко отстает от конкурентов.

MatLab (http://www.mathworks.com/)
Минимальные требования к системе:
- процессор Pentium III, 4, Xeon, Pentium M; AMD Athlon, Athlon XP, Athlon MP;
- 256 Мбайт оперативной памяти (рекомендуется 512 Мбайт);
- 400 Мбайт дискового пространства (только для самой системы MatLab и ее Help);
- операционная система Microsoft Windows 2000 (SP3)/XP.
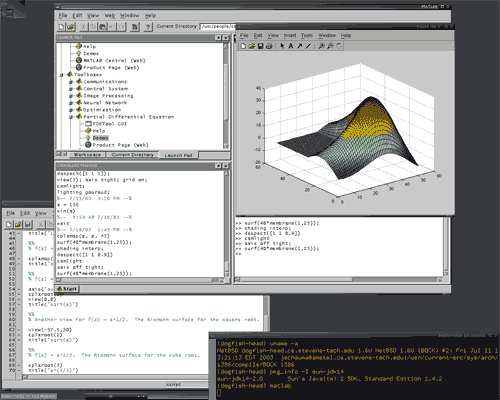
Система MatLab относится к среднему уровню продуктов, предназначенных для символьной математики, но рассчитана на широкое применение в сфере CAE (то есть сильна и в других областях). MatLab — одна из старейших, тщательно проработанных и проверенных временем систем автоматизации математических расчетов, построенная на расширенном представлении и применении матричных операций. Это нашло отражение и в самом названии системы — MATrix LABoratory, то есть матричная лаборатория. Однако синтаксис языка программирования системы продуман настолько тщательно, что данная ориентация почти не ощущается теми пользователями, которых не интересуют непосредственно матричные вычисления.
Несмотря на то что изначально MatLab предназначалась исключительно для вычислений, в процессе эволюции (а сейчас выпущена уже версия 7), в дополнение к прекрасным вычислительным средствам, у фирмы Waterloo Maple по лицензии для MatLab было приобретено ядро символьных преобразований, а также появились библиотеки, которые обеспечивают в MatLab уникальные для математических пакетов функции. Например, широко известная библиотека Simulink, реализуя принцип визуального программирования, позволяет построить логическую схему сложной системы управления из одних только стандартных блоков, не написав при этом ни строчки кода. После конструирования такой схемы можно детально проанализировать ее работу.
В системе MatLab также существуют широкие возможности для программирования. Ее библиотека C Math (компилятор MatLab) является объектной и содержит свыше 300 процедур обработки данных на языке C. Внутри пакета можно использовать как процедуры самой MatLab, так и стандартные процедуры языка C, что делает этот инструмент мощнейшим подспорьем при разработке приложений (используя компилятор C Math, можно встраивать любые процедуры MatLab в готовые приложения).
Библиотека C Math позволяет пользоваться следующими категориями функций:
- операции с матрицами;.
- сравнение матриц;
- решение линейных уравнений;
- разложение операторов и поиск собственных значений;
- нахождение обратной матрицы;
- поиск определителя;
- вычисление матричного экспоненциала;
- элементарная математика;
- функции beta, gamma, erf и эллиптические функции;
- основы статистики и анализа данных;
- поиск корней полиномов;
- фильтрация, свертка;
- быстрое преобразование Фурье (FFT);
- интерполяция;
- операции со строками;
- операции ввода-вывода файлов и т.д.
При этом все библиотеки MatLab отличаются высокой скоростью численных вычислений. Однако матрицы широко применяются не только в таких математических расчетах, как решение задач линейной алгебры и математического моделирования, обсчета статических и динамических систем и объектов. Они являются основой автоматического составления и решения уравнений состояния динамических объектов и систем. Именно универсальность аппарата матричного исчисления значительно повышает интерес к системе MatLab, вобравшей в себя лучшие достижения в области быстрого решения матричных задач. Поэтому MatLab давно уже вышла за рамки специализированной матричной системы, превратившись в одну из наиболее мощных универсальных интегрированных систем компьютерной математики.
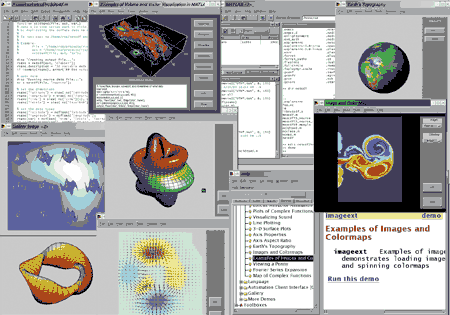
Для визуализации моделирования система MatLab имеет библиотеку Image Processing Toolbox, которая обеспечивает широкий спектр функций, поддерживающих визуализацию проводимых вычислений непосредственно из среды MatLab, увеличение и анализ, а также возможность построения алгоритмов обработки изображений. Усовершенствованные методы графической библиотеки в соединении с языком программирования MatLab обеспечивают открытую расширяемую систему, которая может быть использована для создания специальных приложений, пригодных для обработки графики.
Основные средства библиотеки Image Processing Tollbox:
- построение фильтров, фильтрация и восстановление изображений;
- увеличение изображений;
- анализ и статистическая обработка изображений;
- выделение областей интересов, геометрические и морфологические операции;
- манипуляции с цветом;
- двумерные преобразования;
- блок обработки;
- средство визуализации;
- запись/чтение графических файлов.
Таким образом, систему MatLab можно использовать для обработки изображений, сконструировав собственные алгоритмы, которые будут работать с массивами графики как с матрицами данных. Поскольку язык MatLab оптимизирован для работы с матрицами, в результате обеспечивается простота использования, высокая скорость и экономичность проведения операций над изображениями.
Таким образом, программу MatLab можно использовать для восстановления испорченных изображений, шаблонного распознавания объектов на изображениях или же для разработки каких-либо собственных оригинальных алгоритмов обработки изображений. Библиотека Image Processing Tollbox упрощает разработку высокоточных алгоритмов, поскольку каждая из функций, включенных в эту библиотеку, оптимизирована для максимального быстродействия, эффективности и достоверности вычислений. Кроме того, библиотека обеспечивает разработчика многочисленным инструментарием для создания собственных решений и для реализаций сложных приложений обработки графики. А при анализе изображений использование мгновенного доступа к мощным средствам визуализации помогает моментально увидеть эффекты увеличения, восстановления и фильтрации.
Среди других библиотек системы MatLab можно также отметить System Identification Toolbox — набор инструментов для создания математических моделей динамических систем, основанных на наблюдаемых входных/выходных данных. Особенностью этого инструментария является наличие гибкого пользовательского интерфейса, позволяющего организовать данные и модели. Библиотека System Identification Toolbox поддерживает как параметрические, так и непараметрические методы. Интерфейс системы облегчает предварительную обработку данных, работу с итеративным процессом создания моделей для получения оценок и выделения наиболее значимых данных. Быстрое выполнение с минимальными усилиями таких операций, как открытие/сохранение данных, выделение области возможных значений данных, удаление погрешностей, предотвращение ухода данных от характерного для них уровня.
Наборы данных и идентифицируемые модели организуются графически, что позволяет легко вызвать результаты предыдущих анализов в течение процесса идентификации системы и выбрать следующие возможные шаги процесса. Основной пользовательский интерфейс организует данные для показа уже полученного результата. Это облегчает быстрое сравнение по оценкам моделей, позволяет выделять графическими средствами наиболее значимые модели и исследовать их показатели.
А что касается математических вычислений, то MatLab предоставляет доступ к огромному количеству подпрограмм, содержащихся в библиотеке NAG Foundation Library компании Numerical Algorithms Group Ltd (инструментарий имеет сотни функций из различных областей математики, и многие из этих программ были разработаны широко известными в мире специалистами). Это уникальная коллекция реализаций современных численных методов компьютерной математики, созданных за последние три десятка лет. Таким образом, MatLab вобрала и опыт, и правила, и методы математических вычислений, накопленные за тысячи лет развития математики. Одну только прилагаемую к системе обширную документацию вполне можно рассматривать как фундаментальный многотомный электронный справочник по математическому обеспечению.
Из недостатков системы MatLab можно отметить невысокую интегрированность среды (очень много окон, с которыми лучше работать на двух мониторах), не очень внятную справочную систему (а между тем объем фирменной документации достигает почти 5 тыс. страниц, что делает ее трудно обозримой) и специфический редактор кода MatLab-программ. Сегодня система MatLab широко используется в технике, науке и образовании, но все-таки она больше подходит для анализа данных и организации вычислений, нежели для чисто математических выкладок.
Поэтому для проведения аналитических преобразований в MatLab используется ядро символьных преобразований Maple, а из Maple для численных расчетов можно обращаться к MatLab. Ведь недаром символьная математика Maple вошла составной частью в целый ряд современных пакетов, а численный анализ от MatLab и наборы инструментов (Toolboxes) уникальны. Тем не менее математические пакеты Maple и MatLab — это интеллектуальные лидеры в своих классах, это образцы, определяющие развитие компьютерной математики.
В качестве более простых, но идеологически близких альтернатив программе MatLab можно отметить такие пакеты, как Octave (www.octave.org), KOctave (bubben.homelinux.net/~matti/koctave/) и Genius (www.jirka.org/genius.html).
Octave — это программа числовых вычислений, хорошо совместимая с MatLab. Интерфейс системы Octave, конечно, беднее, и у нее нет таких уникальных библиотек, как у MatLab, зато это очень простая в освоении программа, нетребовательная к системным ресурсам. Распространяется Octave на условиях открытой лицензии с исходным кодом (OpenSource) и может стать хорошим подспорьем для учебных заведений.
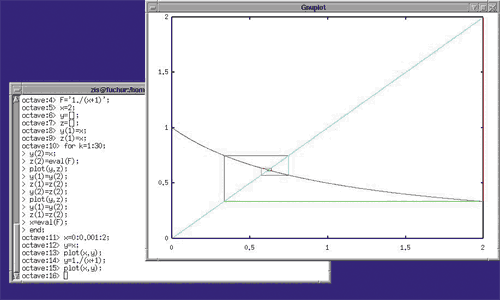
Программа KOctave по сути представляет собой более продвинутый графический интерфейс для системы Octave. В результате использования KOctave система Octave становится полностью похожей на MatLab.
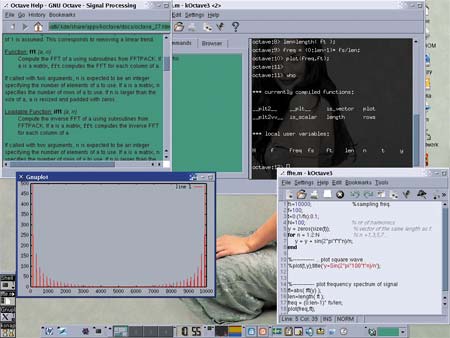
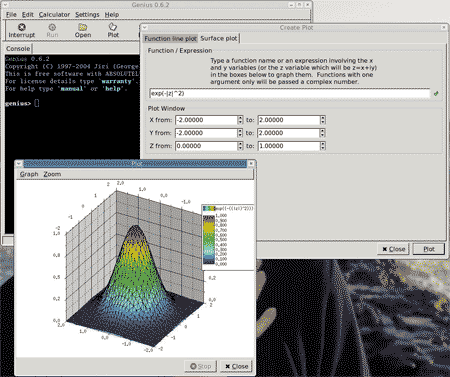
Простенькая математическая программа Genius, естественно, не может поспорить по мощности с именитыми конкурентами, но идеология математических преобразований у нее сходна с MatLab и Maple. Распространяется Genius тоже на условиях открытой лицензии с исходным кодом (OpenSource). Она имеет собственный язык GEL, развитый инструментарий Genius Math Tool и хорошую систему подготовки документов для публикации (с использованием таких языков оформления, как LaTeX, Troff (eqn) и MathML). Очень хороший графический интерфейс программы Genius сделает работу с ней простой и удобной.
MathCad (http://www.mathsoft.com/, http://www.mathcad.com/)
Минимальные требования к системе:
- процессор Pentium II или выше;
- 128 Мбайт оперативной памяти (рекомендуется 256 Мбайт или больше);
- 200-400 Мбайт дискового пространства;
- операционные системы: Windows 98/Me/NT 4.0/2000/XP.
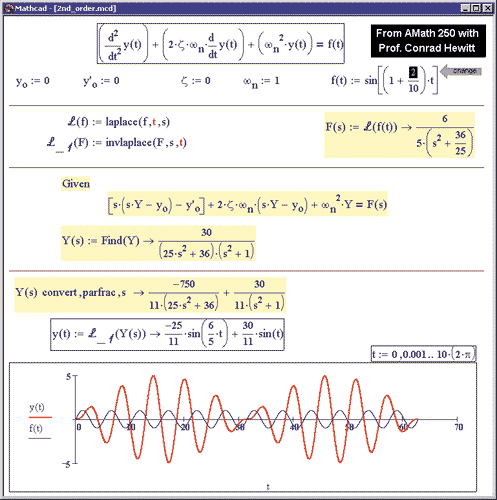
В отличие от мощного и ориентированного на высокоэффективные вычисления при анализе данных пакета MatLab, программа MathCad (текущая версия 13) — это, скорее, простой, но продвинутый редактор математических текстов с широкими возможностями символьных вычислений и прекрасным интерфейсом. MathCad не имеет языка программирования как такового, а движок символьных вычислений заимствован из пакета Maple. Зато интерфейс программы MathCad очень простой, а возможности визуализации богатые. Все вычисления здесь осуществляются на уровне визуальной записи выражений в общеупотребительной математической форме. Пакет имеет хорошие подсказки, подробную документацию, функцию обучения использованию, целый ряд дополнительных модулей и приличную техническую поддержку производителя (как можно видеть по версии продукта, обновление этой программы происходит чаще, чем других, упомянутых в этом обзоре, хотя год выпуска первой версии у них примерно один и тот же — 1996-1997 годы). Однако пока математические возможности MathCad в области компьютерной алгебры намного уступают системам Maple, Mathematica, MatLab и даже малютке Derive. Однако по программе MathCad выпущено много книг и обучающих курсов, в том числе у нас в России. Сегодня эта система стала буквально международным стандартом для технических вычислений и даже многие школьники осваивают и используют MathCad.
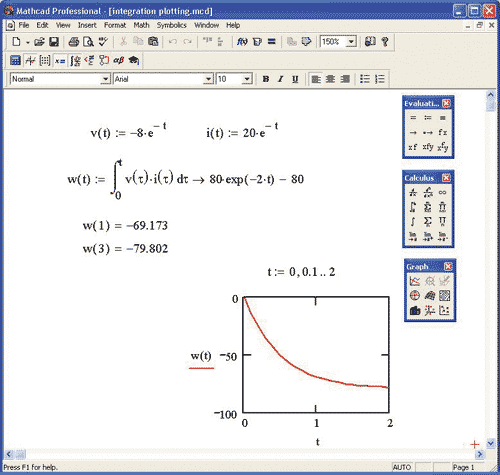
Для небольшого объема вычислений MathCad идеален — здесь все можно проделать очень быстро и эффективно, а затем оформить работу в привычном виде (MathCad предоставляет широкие возможности для оформления результатов, вплоть до публикации в Интернете). Пакет имеет удобные возможности импорта/экспорта данных. Например, можно работать с электронными таблицами Microsoft Excel прямо внутри MathCad-документа.
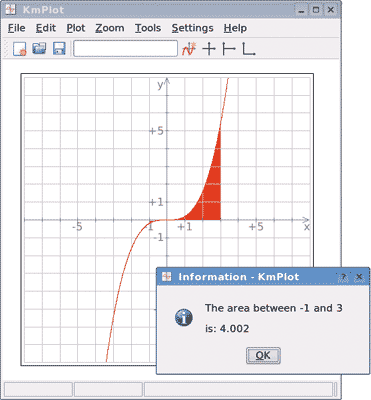
В общем, MathCad — это очень простая и удобная программа, которую можно рекомендовать широкому кругу пользователей, в том числе не очень сведущих в математике, а особенно тем, кто только постигает ее азы.
В качестве более дешевых, простых, но идеологически близких альтернатив программе MathCad можно отметить такие пакеты, как уже упомянутый YaCaS, коммерческую систему MuPAD (http://www.mupad.de/) и бесплатную программу KmPlot (http://edu.kde.org/kmplot/).
Программа KmPlot распространяется на условиях открытой лицензии с исходным кодом (OpenSource). Она очень проста в освоении и подойдет даже школьникам.
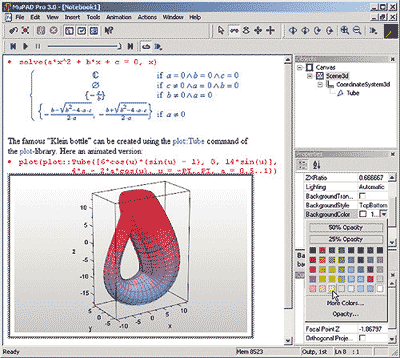
Что касается программы MuPAD, то она представляет собой современную интегрированную систему математических вычислений, при помощи которой можно производить численные и символьные преобразования, а также чертить двумерные и трехмерные графики геометрических объектов. Однако по своим возможностям MuPAD значительно уступает своим маститым конкурентам и является, скорее, системой начального уровня, предназначенной для обучения.
Заключение
Несмотря на то что в области компьютерной математики не наблюдается такого разнообразия, как, скажем, в среде компьютерной графики, за видимой ограниченностью рынка математических программ скрываются их поистине безграничные возможности! Как правило, CAE-системы охватывают практически все области математики и инженерных расчетов.
Когда-то системы символьной математики были ориентированы исключительно на узкий круг профессионалов и работали на больших компьютерах (мэйнфреймах). Но с появлением ПК эти системы были переработаны под них и доведены до уровня массовых серийных программных систем. Сейчас на рынке сосуществуют системы символьной математики самого разного калибра — от рассчитанной на широкий круг потребителей системы MathCad до компьютерных монстров Mathematica, MatLab и Maple, имеющих тысячи встроенных и библиотечных функций, широкие возможности графической визуализации вычислений и развитые средства для подготовки документации.
Отметим, что практически все эти системы работают не только на персональных компьютерах, оснащенных популярными операционными системами Windows, но и под управлением операционных системы Linux, UNIX, Mac OS, а также на КПК. Они давно знакомы пользователям и широко распространены на всех платформах — от наладонника до суперкомпьютера.








