Первые шаги в Maya. Урок 11. Анимация вдоль пути
Технология создания анимации вдоль пути
Привязка объекта к готовой кривой-траектории
Формирование траектории по ключевым положениям объекта
Редактирование траектории движения
Определение поведения объекта при его движении по траектории
Искажение формы объекта при его поворотах
Перемещение объекта по поверхности
Практические примеры создания простых анимаций вдоль пути
Ползущая и оставляющая светящийся след морская звезда
Искажение формы объекта при его поворотах
Если траектория пути имеет резкие повороты, а объект гибкий, то на поворотах он должен деформироваться. Однако в нашей анимации с кубом ничего подобного не происходит. Чтобы убедиться в этом, увеличьте его длину по оси X до 5 и внимательно понаблюдайте за тем, как куб ведет себя на поворотах траектории (рис. 21), только предварительно отмените его перевороты, обнулив параметр SideTwist.
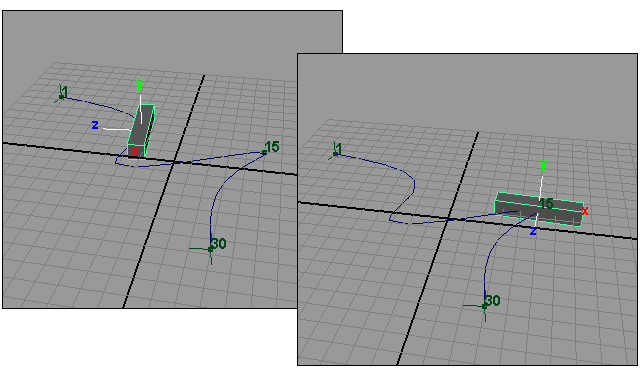
Рис. 21. Поведение куба на поворотах — никакой деформации нет
Деформация объекта при движении вдоль траектории обеспечивается за счет добавления к объекту или к пути Lattice-решетки, правда осуществляется это не рассмотренным нами в предыдущем уроке способом, а несколько иначе. Активируйте первый кадр, выделите куб и примените к нему команду Animate=>MotionPaths=>FlowPathObject (Анимация=>Траектории движения=>Течение объекта по траектории), в результате чего объект окажется заключенным в пространственную решетку (рис. 22). Однако пока это не обеспечит ожидаемую деформацию объекта: решетка искажаться будет, а вот куб, увы, нет (рис. 23). Причина этого кроется не в решетке, а в самом кубе, число разбиений которого по осям явно недостаточно. Выделите куб и увеличьте число разбиений в каждом его направлении до 20 — ситуация тут же изменится (рис. 24).
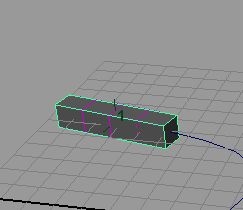
Рис. 22. Появление назначенной объекту Lattice-решетки

Рис. 23. Вид куба и Lattice-решетки на крутом изгибе траектории
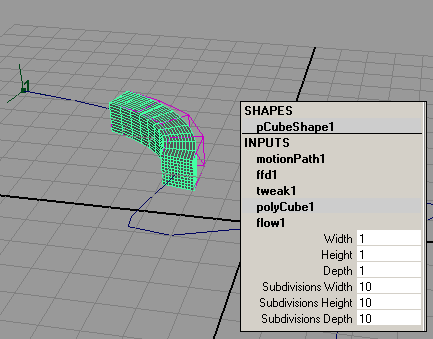
Рис. 24. Результат увеличения числа разбиений куба
А теперь посмотрите, реалистична ли деформация объекта на разных участках траектории. Поскольку объект достаточно длинный, то деформация далеко не всегда выглядит естественно — например в 7, 8 и 9-м кадрах вид куба сложно назвать естественным (рис. 25). Причина нереального искажения его формы кроется в недостаточном числе разбиений решетки по оси X — увеличьте в окне каналов значение параметра SDivisions (Разбиений по S) до 20, и все встанет на свои места (рис. 26).
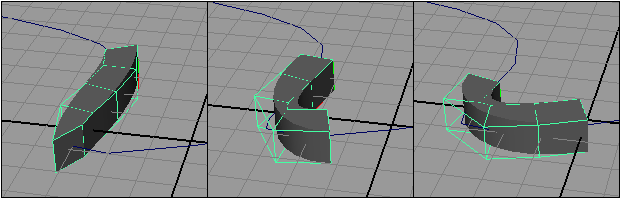
Рис. 25. Исходный вид куба в 7, 8 и 9-м кадрах
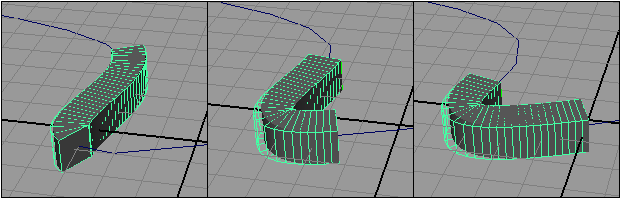
Рис. 26. Изменение характера деформации куба в 7, 8 и 9-м кадрах
А теперь попробуем добиться нужной деформации объекта за счет добавления пространственной решетки не к самому объекту, а к траектории его движения. Для этого вначале нужно удалить решетку объекта, выделив соответствующие ей два узла в окне Outliner и нажав клавишу Del. Выделите куб, щелкните на квадратике справа от команды Animate=>MotionPaths=>FlowPathObject (Анимация=>Траектории движения=>Течение объекта по траектории), выберите тип решетки (Lattice Around) — Curve и увеличьте число разбиений вдоль пути (Divisions Front) до 30 (рис. 27). Вид полученной в итоге Lattice-решетки представлен на рис. 28, где видно, что выбранное число разбиений недостаточно для плавной деформации объекта из-за слишком большой кривизны траектории. Поэтому на таких траекториях более предпочтительно назначать решетку объекту, а не кривой-пути, тем не менее, увеличивая в окне каналов число разбиений Divisions Front, в конечном счете можно добиться нужной кривизны решетки на изгибах траектории (рис. 29).
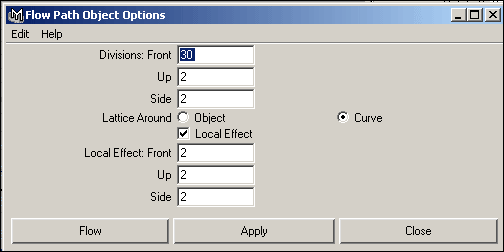
Рис. 27. Настройка параметров пространственной решетки
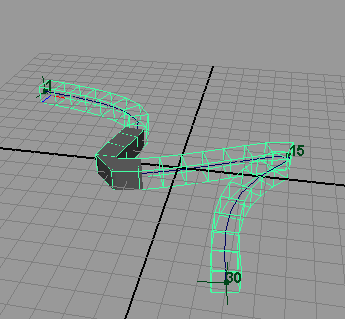
Рис. 28. Деформация куба при исходном разбиении Lattice-решетки
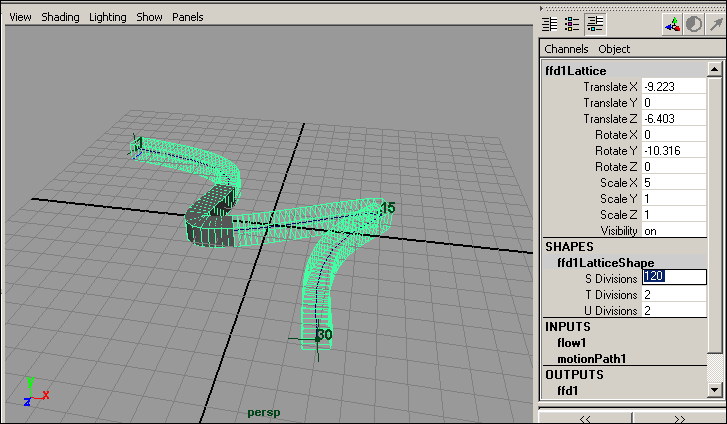
Рис. 29. Деформация куба после увеличения числа разбиений Lattice-решетки
Перемещение объекта по поверхности
Довольно часто объект движется по некоторой плоскости, например по водной поверхности или по земле. А это значит, что его траектория должна быть единым целым с соответствующей поверхностью (а не просто лежать поверх нее), ведь при движении объекта следует учитывать неровности самой поверхности, а не только изгибы траектории. Убедимся в этом на практике.
Вернитесь к нашей рабочей сцене, выделите в окне Outliner узлы пространственной решетки и удалите ее, а затем установите размер куба по оси X равным 1. Смоделируйте холмистую поверхность — создайте NURBS-плоскость с 30 вертикальными и горизонтальными изопармами и обработайте ее инструментом скульптурной деформации (EditNURBS=>SculptSurfaceTool — Редактирование NURBS-поверхностей=>Создание рельефа). Немного сместите плоскость вниз по оси Y так, чтобы она оказалась как бы подложенной под кривую, и проиграйте анимацию — куб, как и ранее, будет двигаться по своей траектории, не обращая никакого внимания на кривизну поверхности и спокойно перемещаясь прямо сквозь холмы (рис. 30).
Рис. 30. Перемещение куба по траектории без учета характера местности
Попробуем изменить ситуацию. Выделите поверхность и преобразуйте ее в активный объект, выбрав команду Modify=>MakeLive (Модифицировать=>Сделать активным) или щелкнув на кнопке Make the selectedObject Live (Сделать активным выделенный объект), расположенной в верхней части экрана (рис. 31). Данная операция необходима для того, чтобы создать кривую, принадлежащую поверхности, а не независимую, как это было ранее. Обратите внимание, что активная плоскость в окне проекций не выделяется и отображается в виде сетки (рис. 32). Выберите один из инструментов для создания кривых и постройте нужную кривую обычным образом. Выйдите из режима Make Live, щелкнув на кнопке Make the selected Object Live, и убедитесь, что построенная кривая, в отличие от независимой кривой, учитывает рельеф местности (рис. 33).
Рис. 31. Кнопка MaketheselectedObjectLive
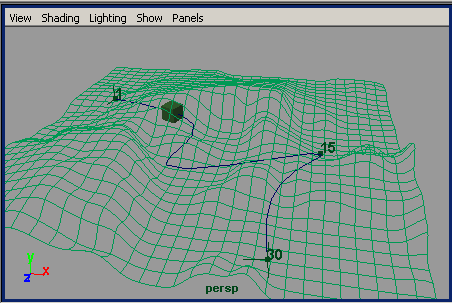
Рис. 32. Отображение активной плоскости в окне проекции
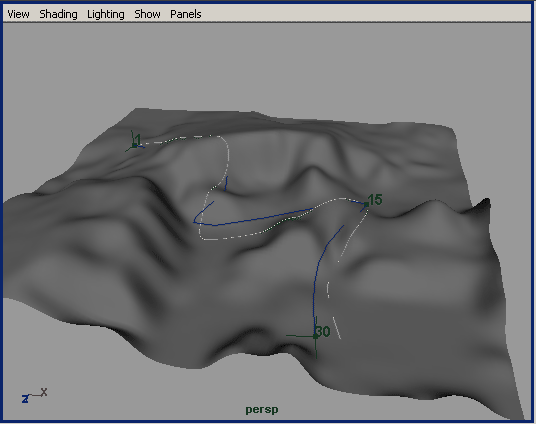
Рис. 33. Вид кривой, принадлежащей плоскости
Чтобы объект можно было связать с новой траекторией, требуется разрушить его связь со старой. Поэтому выделите куб, откройте редактор сцен (команда Window=>Hypergraph), выделите связанный с кубом узел Motion и нажмите клавишу Del. После этого удалите старую траекторию. Для связи куба с новой траекторией выделите его, при нажатой клавише Shift выделите новую кривую (это разумнее сделать в окне Outliner) и примените к ним команду Animate=>MotionPaths=>AttachtoMotionPath (Анимация=>Траектории движения=>Привязать к траектории движения). Проиграв анимацию, вы увидите, что куб перемещается по траектории, поднимаясь на холмы и спускаясь с них (рис. 34). Правда, остается другая проблема — при перемещении по поверхности куб проваливается в нее, что связано с положением его опорной точки, находящейся, как ей и положено, в центре объекта. Выделите куб, переключитесь в режим работы с опорными точками (клавиша Insert) и переместите опорную точку в центр нижней плоскости куба (рис. 35). Теперь куб станет скользить по самой поверхности (без погружения в глубь нее) — рис. 36.
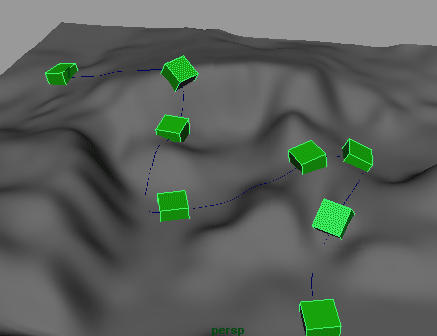
Рис. 34. Движение куба по траектории, связанной с холмистой поверхностью (куб проваливается)
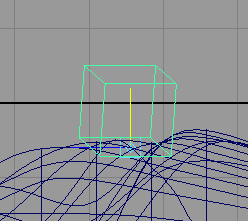
Рис. 35. Перемещение опорной точки куба
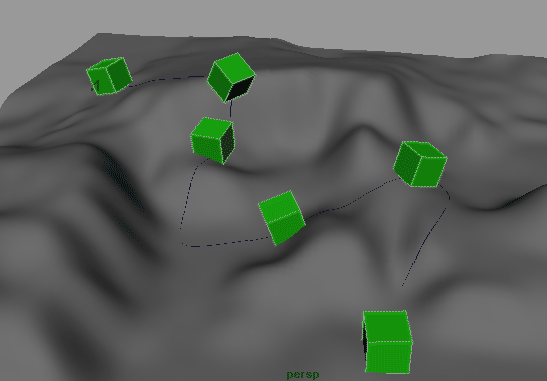
Рис. 36. Скольжение куба по холмистой поверхности