Анатомия беспроводных сетей

Сергей Пахомов

Физический уровень

   Технология расширения спектра методом прямой последовательности (DSSS)

Фазовая модуляция

Скорости передачи протокола IEEE 802.11

   Кодирование DSSS/DPSK

   Кодирование CCK

   Скорость 5,5 Мбит/с

   Скорость 11 Мбит/с

MAC-уровень

Принятие в 1999 году стандарта IEEE 802.11b привело к широкому распространению беспроводных сетей для организации локальных сетей и подключения к Internet.

ежду кабельными сетями Ethernet и беспроводными сетями Radio Ethernet есть много общего, но много и различий. Это и понятно — разные среды передачи данных требуют принципиально различного подхода к способам передачи и кодирования данных, то есть к непосредственной подготовке данных для передачи. Поэтому основные различия между кабельными и беспроводными сетями сконцентрированы на так называемом физическом подуровне (Physical Layer, PHY) и подуровне доступа к среде передачи данных (Medium Access Control, MAC). В соответствии с эталонной моделью сетевых взаимодействий OSI (Open System Interconnection), именно на этих подуровнях данные формируются и кодируются нужным образом для дальнейшей передачи по сети.

Теоретические аспекты функционирования сетей Radio Ethernet регламентированы стандартами IEEE 802.11 и IEEE 802.11b. Именно в этих стандартах определяется порядок организации беспроводных сетей на уровне доступа к среде передачи данных (MAC-уровень) и на физическом уровне (PHY-уровень).

Изначально стандарт IEEE 802.11 предполагал возможность передачи данных по радиоканалу на скорости 1 Мбит/с и опционально на скорости 2 Мбит/с. В более поздней версии — IEEE 802.11b, фактически являющейся дополнением к основному стандарту, определяется скорость передачи 1, 2, 5,5 и 11 Мбит/с.

Подробное описание самого стандарта IEEE 802.11 потребовало бы не просто отдельной статьи — отдельной книги. Судите сами: стандарт IEEE 802.11 изложен более чем на 500 страницах, а его дополнение — 802.11b — это еще 100 страниц текста. Поэтому мы ограничимся лишь поверхностным рассмотрением общих принципов функционирования радиосетей, концентрируя внимание лишь на принципиальных для данной технологии моментах.

Физический уровень

ачнем с рассмотрения физического уровня. Стандартом IEEE 802.11b предусмотрено использование частотного диапазона от 2,4 до 2,4835 ГГц, который предназначен для безлицензионного использования в промышленности, науке и медицине. Разрешение выдается изготовителю и передается заказчику после приобретения продукта в виде сертификата. Здесь следует заметить, что в России использование этого частотного диапазона, кроме сертификатов, требует получения разрешения от Государственного комитета по радиочастотам (ГКРЧ) и Главгоссвязьнадзора РФ.

На физическом уровне стандартом IEEE 802.11 предусмотрено два типа радиоканалов (DSSS и FHSS), которые различаются способом модуляции, но используют одну и ту же технологию расширения спектра.

Технология расширения спектра методом прямой последовательности (DSSS)

Основная идея технологии расширения спектра (Spread Spectrum, SS) заключается в том, чтобы от узкополосного спектра сигнала, возникающего при обычном потенциальном кодировании, перейти к широкополосному спектру. Именно это позволяет значительно повысить помехоустойчивость передаваемых данных. Рассмотрим более детально, как это происходит.

При потенциальном кодировании информационные биты 0 и 1 передаются прямоугольными импульсами напряжений. Из курса математики и физики хорошо известно, что любую функцию и соответственно любой сигнал (ограничения, налагаемые на функцию, мы для простоты опускаем) можно представить в виде дискретного или непрерывного набора гармоник — синусоидальных сигналов с определенным образом подобранными весовыми коэффициентами и частотами. Такое представление называют преобразованием Фурье, а сами частоты гармонических сигналов образуют спектральное разложение функции.

К примеру, при передаче прямоугольного импульса длительностью T спектр сигнала описывается функцией

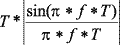
где 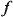  — частота спектральной составляющей (рис. 1).

Несмотря на бесконечный спектр сигнала, наиболее весомые гармоники, то есть вносящие значительный вклад в результирующий сигнал, сосредоточены в небольшой частотной области, ширина которой обратно пропорциональна длительности импульса. Таким образом, с хорошей степенью точности исходный сигнал можно представить как суперпозицию гармоник в спектральной полосе, ширина которой равна длительности импульса T. Соответственно, чем меньше длительность импульса, тем больший спектральный диапазон занимает такой сигнал. Для того чтобы повысить помехоустойчивость передаваемого сигнала, то есть увеличить вероятность безошибочного распознавания сигнала на приемной стороне в условиях шума, можно воспользоваться методом перехода к широкополосному сигналу, добавляя избыточность в исходный сигнал. Для этого в каждый передаваемый информационный бит «встраивают» определенный код, состоящий из последовательности так называемых чипов (рис. 2).

Фактически информационный бит, представляемый прямоугольным им­пульсом, разбивается на последовательность более мелких импульсов-чипов. В результате спектр сигнала значительно уширяется, так как ширину спектра можно с хорошей степенью точности считать обратно пропорциональной длительности одного чипа. Такие кодовые последовательности часто называют шумоподобными кодами. Дело в том, что наряду с уширением спектра сигнала уменьшается и спектральная плотность энергии. То есть энергия сигнала как бы «размазывается» по всему спектру. Результирующий сигнал становится шумоподобным в том смысле, что его теперь трудно отличить от естественного шума. Возникает вопрос — для чего усложнять первоначальный сигнал, если в результате он становится неотличимым от шума? Дело в том, что кодовые последовательности чипов обладают уникальным свойством автокорреляции. Попробуем на интуитивном уровне пояснить, в чем смысл корреляции. Под корреляцией в математике понимают степень взаимоподобия двух функций, то есть насколько две различные функции похожи друг на друга. Соответственно под автокорреляцией понимается степень подобия функции самой себе в различные моменты времени. Например, если некоторая функция зависит (меняется) от времени и эта зависимость выражается в виде 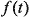, то можно рассмотреть функцию в некоторый момент времени 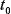и в момент времени 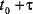. Степень соответствия этих двух функций друг другу в различные моменты времени и называется автокорреляцией. Оказывается, что можно подобрать такую последовательность чипов, для которой функция автокорреляции, отражающая степень подобия функции самой себе через определенный временной интервал, будет иметь резко выраженный пик лишь для одного момента времени. То есть функция будет подобна самой себе только для одного момента времени и совсем не похожа на себя для всех остальных моментов времени. Одна из наиболее известных (но не единственная) таких последовательностей — код Баркера длиной в 11 чипов: 11100010010. Коды Баркера обладают наилучшими среди известных псевдослучайных последовательностей свойствами шумоподобности, что и обусловило их широкое применение. Для передачи единичного и нулевого символов сообщения используются соответственно прямая и инверсная последовательности.

Для упрощенного вычисления автокорреляционной функции последовательности Баркера можно рассчитать разницу между числом совпадений и несовпадений между отдельными чипами последовательности при их циклическом почиповом сдвиге относительно друг друга.

Как видно из табл. 1, последовательность Баркера обладает ярко выраженным автокорреляционным пиком, соответствующим наложению функции самой на себя. Проведя аналогичные расчеты, нетрудно убедиться, что другие последовательности не обладают подобным свойством, то есть имеют несколько пиков корреляции, которые значительно снижают помехоустойчивость передаваемого сигнала.

В приемнике полученный сигнал умножается на код Баркера (вычисляется корреляционная функция сигнала), в результате он становится узкополосным, поэтому его фильтруют в узкой полосе частот, равной удвоенной скорости передачи. Любая помеха, попадающая в полосу исходного широкополосного сигнала, после умножения на код Баркера, наоборот, становится широкополосной, поэтому в узкую информационную полосу попадает лишь часть помехи, по мощности примерно в 11 раз меньшая чем помеха, действующая на входе приемника.

Итак, основной смысл использования кодов Баркера заключается в том, чтобы, имея возможность передавать сигнал практически на уровне помех, гарантировать высокую степень достоверности принимаемой информации.

Как известно, радиоволны приобретают способность переносить информацию в том случае, если они определенным образом модулируются. При этом необходимо, чтобы модуляция синусоидального несущего сигнала соответствовала требуемой последовательности информационных бит. Существует три основных типа модуляции: амплитудная, частотная и фазовая. В стандарте IEEE 802.11 для передачи сигналов используют фазовую модуляцию, поэтому остановимся на ней более подробно.

Фазовая модуляция

азличают два типа фазовой модуляции: собственно фазовую и относительную фазовую модуляцию. При фазовой модуляции (Phase Shift Key, PSK) для передачи логических нулей и единиц используют сигналы одной и той же частоты и амплитуды, но смещенные относительно друг друга по фазе. Например, логический нуль передается синфазным сигналом, а единица — сигналом, сдвинутым по фазе на 180° (рис. 3).

Если изменение фазы может принимать всего два значения, то говорят о двоичной фазовой модуляции (Binary Phase Shift Key, BPSK). Математически сигнал, соответствующий логическому нулю, можно представить как 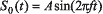, а сигнал, соответствующий логической единице, — как 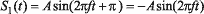. Тогда модулированный сигнал можно записать в виде: 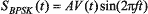, где V(t) — управляющий сигнал, принимающий значения +1 и –1. Причем значение сигнала +1 соответствует логическому нулю, а значение сигнала –1 — логической единице.

Изменение фазы может иметь и более двух значений, например четыре (0, 90, 180 и 270°). В этом случае говорят о так называемой квадратурной фазовой модуляции (Quadrature Phase Shift Key, QPSK) — (рис. 4). Чтобы понять происхождение этого термина, рассмотрим общий вид сигнала, модулированного по фазе: .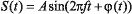

С учетом простейших тригонометрических соотношений данную формулу несложно привести к виду: .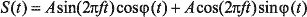

Из полученного выражения видно, что исходный сигнал можно представить в виде суммы двух гармонических составляющих, смещенных друг относительно друга по фазе на 90°, так как

.

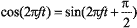В передатчике, производящем модуляцию, одна из этих составляющих синфазна сигналу генератора, а вторая находится в квадратуре по отношению к этому сигналу (отсюда — квадратурная модуляция). Синфазная составляющая обозначается как I (In Phase), а квадратурная — как Q (Quadrature).

Исходный сигнал несложно преобразовать:

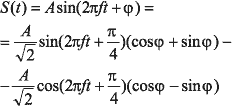
Если ввести обозначения 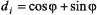; 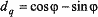, то получим следующий вид сигнала:

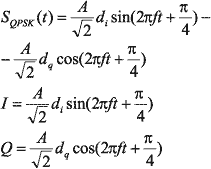
Кодирующие сигналы d_i и d_q могут принимать значения +1 и –1; учитывая, что 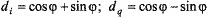, получим соотношение между сдвигом фазы и кодирующими сигналами, приведенное в табл. 2.

При реализации квадратурной фазовой модуляции входной поток бит преобразуется в кодирующую последовательность {d_k} так, что логическому нулю соответствует кодирующий бит +1, а логической единице — кодирующий бит –1. После этого кодирующий поток разделяется на четные и нечетные биты. Четные биты поступают в I-канал, а нечетные — в Q-канал. Причем длительность каждого управляющего импульса d_i и d_q в два раза больше длительности исходного импульса d_k.

Управляющие биты di модулируют по фазе сигнал 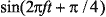, а биты d_q модулируют ортогональный сигнал (смещенный по фазе на 90°), то есть 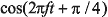. После этого оба сигнала складываются и образуется модулированный сигнал (рис. 5).

В приведенной выше схеме квадратурной фазовой модуляции фаза результирующего сигнала может изменяться только каждые 2T секунд.

Отличительной особенностью квадратурной фазовой модуляции является наличие четырех дискретных состояний сигнала, отвечающих различным фазам. Это позволяет закодировать в одном дискретном состоянии последовательность двух информационных бит (так называемый дибит). Действительно, последовательность двух бит может иметь всего четыре различные комбинации: 00, 01, 10 и 11. Следовательно, ровно в два раза повышается и скорость передачи данных, то есть бодовая скорость в два раза больше битовой (1 Бод = 2 бит/с).

Учитывая, что кодирующему биту +1 отвечает логический нуль, а кодирующему биту –1 — логическая единица, и, принимая во внимание соответствие между фазой сигнала и значениями d_i и d_q, получим таблицу соответствия между входными дибитами и фазами модулированного сигнала (табл. 3).

Возможные дискретные состояния сигнала принято изображать на векторной диаграмме состояния или на плоскости сигнального созвездия.

При использовании векторной диаграммы состояния каждому значению сигнала ставится в соответствие вектор, длина которого — это условная амплитуда сигнала, а угол поворота вектора относительно горизонтальной оси — это фаза сигнала. То есть векторная диаграмма — это не что иное, как изображение векторов состояния в полярной системе координат. Примеры диаграмм состояния для двоичной и квадратурной фазовой модуляций показаны на рис. 6.

Более широкое распространение получил способ отображения различных состояний сигала на сигнальном созвездии. Сигнальное созвездие — это декартова система координат, по оси абсцисс которой откладываются значения кодирующего сигнала d_i (ось I), а по оси ординат — значения кодирующего сигнала d_q (ось Q). В случае двоичной фазовой модуляции плоскость вырождается в прямую, вдоль которой откладываются значения кодирующего сигнала d_k. В этом случае на сигнальном созвездии располагаются всего две точки, отвечающие значениям кодирующих битов +1 и –1. Эти две точки соответствуют всем возможным состояниям сигнала.

В случае QPSK-модуляции сигнальное созвездие состоит уже из четырех точек с координатами (+1, +1), (+1, –1), (–1, +1), (–1, –1). Эти четыре точки соответствуют четырем возможным дибитам и образуют совокупность всех возможных состояний сигнала (рис. 7).

Несмотря на кажущуюся простоту метода фазовой модуляции ему присущи некоторые недостатки, связанные с трудностями технической реализации.

Один из недостатков связан с тем, что в случае квадратурной фазовой модуляции при одновременной смене символов в обоих каналах модулятора (с +1, –1 на –1, +1 или с +1, +1 на –1, –1) в сигнале QPSK происходит скачок фазы на 180°. Такие скачки фазы, имеющие место и при обыкновенной двухфазной модуляции, вызывают паразитную амплитудную модуляцию огибающей сигнала. В результате этого при прохождении сигнала через узкополосный фильтр возникают провалы огибающей до нуля. Такие изменения сигнала нежелательны, поскольку приводят к увеличению энергии боковых полос и помех в канале связи.

Для того чтобы избежать этого нежелательного явления, прибегают к так называемой квадратурной фазовой модуляции со сдвигом (Offset QPSK, OQPSK). При таком типе модуляции формирование сигнала в квадратурной схеме происходит так же, как и в модуляторе QPSK, за исключением того, что кодирующие биты в Q-канале имеют временную задержку на длительность одного элемента Т. Изменение фазы при таком смещении кодирующих потоков определяется лишь одним элементом последовательности, а не двумя. В результате скачки фазы на 180° отсутствуют, поскольку каждый элемент последовательности, поступающий на вход модулятора синфазного или квадратурного канала, может вызвать изменение фазы на 0, 90 или 270° (–90°).

Другим, более серьезным недостатком фазовой модуляции является то обстоятельство, что при декодировании сигнала приемник должен определять абсолютное значение фазы сигнала, так как в фазовой модуляции информация кодируется именно абсолютным значением фазы сигнала. Для этого необходимо, чтобы приемник имел информацию об «эталонном» синфазном сигнале передатчика. Тогда путем сравнения принимаемого сигнала с эталонным можно определять абсолютный сдвиг фазы. Следовательно, необходимо каким-то способом синхронизировать сигнал передатчика с эталонным сигналом приемника (по этой причине фазовая модуляция получила название синхронной). Реализация синхронной передачи достаточно сложна, поэтому более широкое распространение получила разновидность фазовой модуляции, называемая относительной фазовой модуляцией (Differential Phase Shift Keying, DPSK). При относительной фазовой модуляции (также называемой относительной фазовой манипуляцией) кодирование информации происходит за счет сдвига фазы по отношению к предыдущему состоянию сигнала. Фактически приемник должен улавливать не абсолютное значение фазы принимаемого сигнала, а лишь изменение этой фазы. То есть информация кодируется изменением фазы. Естественно, такая модуляция уже не является синхронной и проще реализуется. Во всем остальном DPSK-модуляция не отличается от PSK-модуляции.

Для технической реализации DPSK-модуляции входной поток информационных бит первоначально преобразуется, а затем подвергается обычной фазовой модуляции. Если необходимо, чтобы скачки по фазе происходили при появлении логического нуля, то преобразование исходной последовательности сводится к следующему: при появлении нуля происходит преобразование сигнала на инверсный, а при появлении единицы сигнал не меняется. Для примера рассмотрим преобразование 11-чиповой последовательности Баркера по описанному правилу (табл. 4).

Данный алгоритм можно записать как логическую операцию неравнозначности над исходной последовательностью и преобразованной последовательностью, задержанной на один бит (смещенной по времени) (рис. 8). Математически это записывается в виде формулы: 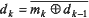, где m_k  — исходная последовательность, d_k — преобразованная последовательность (при расчетах предполагается, что первый бит преобразованной последовательности равен 1).

Аналогично производится преобразование входящей последовательности для получения относительной фазовой модуляции и во втором случае, то есть когда требуется, чтобы фаза сигнала менялась каждый раз при появлении на входе логической единицы. Однако в этом случае формула преобразования будет выглядеть так: 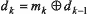. Пример получения двоичной относительной фазовой модуляции DBPSK показан на рис. 9.

Скорости передачи протокола IEEE 802.11

Кодирование DSSS/DPSK

Столь пристальное внимание фазовой модуляции мы уделили потому, что именно она используется в протоколе IEEE 802.11 для кодирования данных. При передаче данных на скорости 1 Мбит/с используется двоичная относительная фазовая модуляция (DBPSK). При этом сам информационный единичный бит передается 11-чиповой последовательностью Баркера, а нулевой бит — инверсной последовательностью Баркера. Соответственно, сама относительная фазовая модуляция применяется именно к отдельным чипам последовательности.

Учитывая, что ширина спектра прямоугольного импульса обратно пропорциональна его длительности, а точнее, 2/T (см. рис. 1), нетрудно посчитать, что при информационной скорости 1 Мбит/с скорость следования отдельных чипов последовательности Баркера составит 11 Мчип/с, а ширина спектра такого сигнала — 22 МГц, так как длительность одного чипа составляет 1/11 мкс.

Как уже отмечалось, информационная скорость 1 Мбит/с является обязательной в стандарте IEEE 802.11 (basic access rate), но опционально возможна передача и на скорости 2 Мбит/с (enhanced access rate). Для передачи данных на такой скорости также используется относительная фазовая модуляция, но уже квадратурная (DQPSK). Это позволяет в два раза повысить информационную скорость передачи. При этом ширина самого спектра остается прежней, то есть 22 МГц.

В дополнении к стандарту IEEE 802.11, то есть в стандарте 802.11b, кроме скоростей 1 и 2 Мбит/с обязательными являются также скорости 5,5 и 11 Мбит/с. Для работы на таких скоростях используется уже несколько иной способ уширения спектра.

Кодирование CCK

В настоящей версии стандарта IEEE 802.11b используется несколько способов кодирования с использованием комплементарных кодов (Complementary Code Keying, CCK). Их рассмотрение достаточно сложно с математической точки зрения, поэтому мы лишь поверхностно коснемся этой темы.

Если говорить в общих чертах, то использование CCK-кодов позволяет кодировать 8 бит на один символ при скорости 11 Мбит/с и 4 бита на символ при скорости 5,5 Мбит/с. При этом сами кодовые последовательности являются 8-чиповыми и при скорости передачи 11 Мбит/с кодирование 8 бит на символ соответствует символьной скорости 1,385 мегасимволов в секунду (11/8 = 1,385). Аналогичная символьная скорость используется и при скорости передачи 5,5 бит/с, так как при такой скорости в одном символе кодируется только 4 бита.

Особый интерес представляют сами CCK-последовательности. Прежде всего определим, что следует называть CСK-последовательностью. Для двух ССК-последовательностей равной длины сумма их автокорреляционных функций для любого циклического сдвига, отличного от нуля, всегда равна нулю.

Исходя из того, что автокорреляционная функция определяется как сумма попарных произведений последовательности при ее циклическом сдвиге, обозначим через ai элементы первой последовательности, а через b_i — элементы второй. Тогда автокорреляционная функция для первой последовательности длиной n для циклического сдвига на j элементов запишется как:

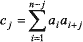
Аналогично, для второй последовательности автокорреляционная функция примет вид:

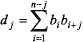
При этом две последовательности будут называться комплементарными, если

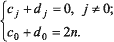
Аналогично тому, как были рассмотрены комплементарные двоичные последовательности, элементы которых принимали только значения +1 и –1 (табл. 5), можно определить комплементарные последовательности на множестве комплексных чисел или многофазовые последовательности Polyphase Codes.

В стандарте IEEE 802.11b речь идет как раз о таких комплексных комплементарных последовательностях, содержащих элементы с четырьмя различными фазами, то есть о комплементарных последовательностях, определенных на множестве комплексных элементов {1, -?1, j, -j}. Сами комплементарные последовательности, как и прежде, используются для уширения спектра сигнала (DSSS) и являются 8-чиповыми. Скорость передачи при этом составляет 11 Мчип/с, что дает скорость 1,375 мегасимволов в секунду. При этом ширина спектра сигнала, как и при использовании последовательностей Баркера, составляет 22 МГц, что позволяет использовать в частотном диапазоне от 2,4 до 2,4835 ГГц три неперекрывающиеся частотные полосы.

Сами комплементарные 8-чиповые комплексные последовательности образуются по следующей формуле:

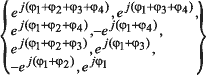
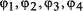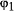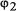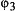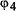Значения фаз определяются последовательностью входных битов, причем значение выбирается по первому дибиту, — по второму,  — по третьему и  — по четвертому. Таким образом, для однозначного определения СКК-последовательности требуется 8 бит входных данных. Обратим внимание, что фаза 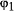, а соответственно и член 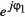, присутствуют во всех членах последовательности. Фактически это означает сдвиг по фазе всех членов последовательности на один и тот же угол, то есть поворот вектора, задающего последовательность, или символа, определяемого последовательностью. По этой причине первый дибит данных — как для скорости передачи 5,5 Мбит/с, так и для скорости 11 Мбит/с — задает сдвиг целого символа по фазе по отношению к фазе предыдущего переданного символа.

Скорость 5,5 Мбит/с

Для скорости 5,5 Мбит/с в одном символе кодируется 4 бита, то есть два дибита (d0 – d3). Первый дибит определяет фазовый сдвиг четных и нечетных символов в соответствии с табл. 6.

Следующий дибит, то есть биты d2, d3, определяет остальные фазы CCK-последовательности по формулам:

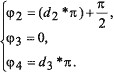
Рассмотрим, к примеру, последовательность данных 11011000. Разбивая ее на пару четырехбитовых символов 1101 и 1000, первый из которых нечетный, а второй — четный, получим, что для нечетного символа , , 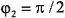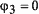и 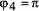. Тогда комплексная CKK-последовательность примет вид: {-j, -1, -j, 1, j, 1, -j, 1}.

Аналогично для второго символа 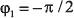, , 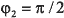, , 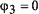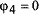а CKK-последовательность имеет вид: {1, –j, 1, j, 1, –j, –1, –j}. Как нетрудно заметить, обе последовательности сдвинуты друг относительно друга на 90°, точнее, вторая последовательность, соответствующая четному символу, сдвинута относительно первой последовательности на

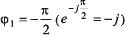
Скорость 11 Мбит/с

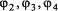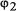При скорости 11 Мбит/с в одном символе кодируется одновременно 8 бит данных. При этом первый дибит последовательности данных, как и прежде, задает сдвиг фазы при относительной фазовой модуляции целого символа в зависимости от того, четный он или нечетный, точно так же, как и для скорости 5,5 Мбит/с. Остальные три дибита 8-битовой последовательности данных определяют фазы , причем значение выбирается по второму дибиту, 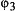 — по третьему и 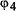— по четвертому. Значение сдвига фаз определяется по табл. 7.

Если, к примеру, на вход поступает последовательность 8 бит данных 00111011 и символ является четным, то, пользуясь таблицами, найдем:

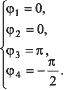
Тогда сама CCK-последовательность примет вид: {j, j, -j, j, -1, -1, -1, 1}.

С помощью описанных выше алгоритмов кодирования можно представить схему CKK-модулятора (рис. 10).

Как уже отмечалось, для задания CKK-последовательности используются только 6 бит данных (второй, третий и четвертый дибиты). Первый дибит определяет сдвиг по фазе всего символа и используется в относительной фазовой модуляции. Шесть бит данных могут иметь 64 различные комбинации (26 = 64). Поэтому говорят, что в протоколе IEEE 802.11b при кодировании каждого символа используется одна из 64 возможных восьмиразрядных CKK-последовательностей. Последовательности, формируемые в CKK-модуляторе, в дальнейшем поступают на I- и Q-каналы QPSK-модулятора.

В заключение обзора различных методов модуляции на физическом уровне, принятых в стандарте IEEE 802.11b, можно составить итоговую таблицу (табл. 8).

MAC-уровень

а МАС-уровне определяются базовые структуры архитектуры сети и перечень услуг, предоставляемых этим уровнем. Стандартом определяются два основных типа архитектуры сетей: Ad Нос и Infrastructure Mode.

В режиме Ad Hoc (рис. 11), который называют также IBSS (Independent Basic Service Set) или режим Peer to Peer (точка-точка), станции непосредственно взаимодействуют друг с другом. Для этого режима требуется минимум оборудования — каждая станция должна быть оснащена беспроводным адаптером. При такой конфигурации не требуется создания какой-либо сетевой инфраструктуры. Основным недостатком режима Ad Hoc является ограниченный диапазон действия, или радиус, возможной сети, а также возможность подключения к внешней сети (например, к Интернету).

В режиме Infrastructure Mode (рис. 12) станции взаимодействуют друг с другом не напрямую, а через точку доступа (Access Point), которая выполняет в беспроводной сети роль своеобразного концентратора (аналогично тому, как это происходит в традиционных кабельных сетях). Рассматривают два режима взаимодействия с точками доступа: BSS (Basic Service Set) и ESS (Extended Service Set). В режиме BSS все станции связы­ваются между собой только через точку доступа, которая может выполнять также функцию моста с внешней сетью. В рас­ширенном режиме — ESS существует ин-фраструктура нескольких сетей BSS, при­чем сами точки доступа взаимодействуют друг с другом, что позволяет передавать трафик от одной BSS к другой. Сами точки доступа соединяются между собой либо с помощью сегментов кабельной сети, либо с помощью радиомостов.

Для доступа к среде передачи данных в беспроводных сетях стандарта IEEE 802.11b используется метод коллективного доступа с обнаружением несущей и избежанием коллизий (Carrier Sense Multiple Access / Collision Avoidance, CSMA/CA). Собственно, метод даже по названию напоминает технологию коллективного доступа, используемую в сетях Ethernet. Действительно, в сетях Ethernet используется метод коллективного доступа с опознанием несущей и обнаружением коллизий (carrier-sense-multiply-access with collision detection, CSMA/CD). Единственное отличие заключено во второй части метода — вместо обнаружения коллизий используется технология избежания коллизий.

Перед тем как послать данные в «эфир», станция сначала посылает специальное сообщение, называемое RTS (Ready To Send), которое трактуется как готовность данного узла к отправке данных. Данное RTS-сообщение содержит информацию о продолжительности предстоящей передачи и адресате и доступно всем узлам в сети. Это позволяет другим узлам задержать передачу на время, равное объявленной длительности сообщения. Приемная станция, получив сигнал RTS, отвечает посылкой сигнала CTS (Clear To Send), соответствующего готовности станции к приему информации. После этого передающая станция посылает пакет данных, а приемная станция должна передать кадр ACK, подтверждающий безошибочный прием. Если АСК не получен, попытка передачи пакета данных будет повторена. Таким образом, с использованием такого четырехэтапного протокола передачи данных (4-Way Handshake) реализуется регламентирование коллективного доступа с минимизацией вероятности возникновения коллизий (рис. 13).

Каждый пакет данных (рис. 14) снабжается контрольной суммой CRC, что гарантирует обнаружение битых кадров при приеме. Пакетная фрагментация, определяемая в стандарте, предусматривает разбивку большого пакета данных на малые порции. Такой подход позволяет снизить вероятность повторной передачи кадра данных, поскольку с увеличением размера кадра возрастает и вероятность ошибки при его передаче. Если же переданный кадр оказался битым, то в случае малого размера кадра передающей станции придется повторить только малый фрагмент сообщения.

Спецификация пакетирования данных, предусмотренная стандартом, предписывает разбивку данных на пакеты, снабженные контрольной и адресной информацией длиной в 30 байт, блока данных длиной до 2048 байт и 4-байтного CRC-блока. Стандарт рекомендует использовать пакеты длиной 1500 или 2048 байт.

Конечно, в небольшой статье невозможно описать все особенности протокола 802.11b, поэтому еще раз подчеркнем, что мы старались сконцентрировать ваше внимание лишь на основных, принципиальных моментах, позволяющих в общих чертах понять принципы функционирования беспроводных сетей. Нерассмотренными остались такие важные моменты, как обеспечение безопасности данных, включающее аутентификацию узла, входящего в сеть, а также шифрование данных.

КомпьютерПресс 7'2002