ДНК-логика как основа биокомпьютера
Преимущества ДНК в компьютерных технологиях
Базовые операции над ДНК-молекулами
DNA Logic — это технология ДНК-вычислений, которая сегодня находится в зачаточном состоянии, однако в будущем на нее возлагаются большие надежды. Биологические нанокомпьютеры, вживляемые в живые организмы, пока видятся нам как нечто фантастическое, нереальное. Но то, что нереально сегодня, уже завтра может оказаться чем-то обыденным и настолько естественным, что трудно будет представить, как без этого можно было обходиться в прошлом.
Итак, ДНК-вычисления — это раздел области молекулярных вычислений на границе молекулярной биологии и компьютерных наук. Основная идея ДНК-вычислений — построение новой парадигмы, создание новых алгоритмов вычислений на основе знаний о строении и функциях молекулы ДНК и операций, которые выполняются в живых клетках над молекулами ДНК при помощи различных ферментов. К перспективам ДНК-вычислений относится создание биологического нанокомпьютера, который будет способен хранить терабайты информации при объеме в несколько микрометров. Такой компьютер можно будет вживлять в клетку живого организма, а его производительность будет исчисляться миллиардами операций в секунду при энергопотреблении не более одной миллиардной доли ватта.
Преимущества ДНК в компьютерных технологиях
Для современных процессоров и микросхем в качестве строительного материала используется кремний. Но возможности кремния не беспредельны, и в конечном счете мы подойдем к той черте, когда дальнейший рост вычислительной мощности процессоров окажется исчерпан. А потому перед человечеством уже сейчас остро стоит проблема поиска новых технологий и материалов, которые смогли бы в будущем заменить кремний.
Молекулы ДНК могут оказаться тем самым материалом, который впоследствии заменит кремниевые транзисторы с их бинарной логикой. Достаточно сказать, что всего один фунт (453 г) ДНК-молекул обладает емкостью для хранения данных, которая превосходит суммарную емкость всех современных электронных систем хранения данных, а вычислительная мощность ДНК-процессора размером с каплю будет выше самого мощного современного суперкомпьютера.
Более 10 триллионов ДНК-молекул занимают объем всего в 1 см3. Однако такого количества молекул достаточно для хранения объема информации в 10 Тбайт, при этом они могут производить 10 трлн операций в секунду.
Еще одно преимущество ДНК-процессоров в сравнении с обычными кремниевыми процессорами заключается в том, что они могут производить все вычисления не последовательно, а параллельно, что обеспечивает выполнение сложнейших математических расчетов буквально за считаные минуты. Традиционным компьютерам для выполнения таких расчетов потребовались бы месяцы и годы.
Строение молекул ДНК
Как известно, современные компьютеры работают с бинарной логикой, подразумевающей наличие всего двух состояний: логического нуля и единицы. Используя двоичный код, то есть последовательность нулей и единиц, можно закодировать любую информацию. В молекулах ДНК имеется четыре базовых основания: аденин (A), гуанин (G), цитозин (C) и тимин (T), связанных друг с другом в цепочку. То есть молекула ДНК (одинарная цепочка) может иметь, например, такой вид: ATTTACGGCC — здесь используется не двоичная, а четверичная логика. И подобно тому, как в двоичной логике любую информацию можно закодировать в виде последовательности нулей и единиц, в молекулах ДНК можно кодировать любую информацию путем сочетания базовых оснований.
Базовые основания в молекулах ДНК находятся друг от друга на расстоянии 0,34 нанометра, что обусловливает их огромную информативную емкость — линейная плотность составляет 18 Мбит/дюйм. Если же говорить о поверхностной информативной плотности, предполагая, что на одно базовое основание приходится площадь в 1 квадратный нанометр, то она составляет более миллиона гигабит на квадратный дюйм. Для сравнения отметим, что поверхностная плотность записи современных жестких дисков составляет порядка 7 Гбит/дюйм 2.
Другое важное свойство ДНК-молекул заключается в том, что они могут иметь форму регулярной двойной спирали, диаметр которой составляет всего 2 нм. Такая спираль состоит из двух цепей (последовательностей базовых оснований), причем содержание первой цепи строго соответствует содержанию второй.
Это соответствие достигается благодаря наличию водородных связей между направленными навстречу друг другу основаниями двух цепей — попарно G и C или A и T. Описывая это свойство двойной спирали, молекулярные биологи говорят, что цепи ДНК комплементарны за счет образования пар G-C и A-T.
К примеру, если последовательность S записывается как ATTACGTCG, то дополняющая ее последовательность S’ будет иметь вид TAATGCAGC.
Процесс соединения двух одинарных цепочек ДНК путем связывания комплементарных оснований в регулярную двойную спираль называется ренатурацией, а обратный процесс, то есть разъединение двойной цепочки и получение двух одинарных цепочек, — денатурацией (рис. 1).
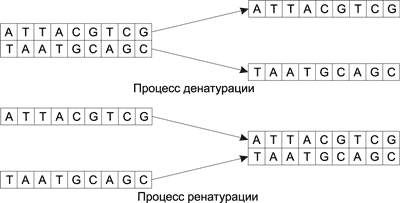
Рис. 1. Процессы ренатурации и денатурации
Комплементарная особенность строения ДНК-молекул может использоваться при ДНК-вычислениях. К примеру, на основе дополняющих друг друга последовательностей можно реализовать мощнейший механизм коррекции ошибок, который чем-то напоминает технологию зеркалирования данных RAID Level 1.
Базовые операции над ДНК-молекулами
Для различных манипуляций над ДНК-молекулами используются различные энзимы (ферменты). И точно так же, как современные микропроцессоры имеют набор базовых операций типа сложения, сдвига, логических операций AND, OR и NOT NOR, ДНК-молекулы под воздействием энзимов могут выполнять такие базовые операции, как разрезание, копирование, вставка и др. Причем все операции над ДНК-молекулами можно производить параллельно и независимо от других операций, к примеру дополнение цепочки ДНК осуществляется при воздействии на исходную молекулу ферментов — полимераз. Для работы полимеразы необходимо наличие одноцепочечной молекулы (матрицы), определяющей добавляемую цепочку по принципу комплементарности, праймера (небольшого двухцепочечного участка) и свободных нуклеотидов в растворе. Процесс дополнения цепочки ДНК показан на рис. 2.
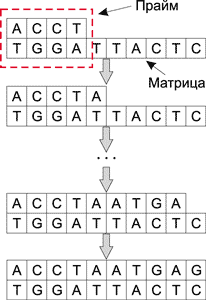
Рис. 2. Процесс дополнения цепочки ДНК
при воздействии на исходную молекулу полимеразы
Существуют полимеразы, которым не требуются матрицы для удлинения цепочки ДНК. Например, терминальная трансфераза добавляет одинарные цепочки ДНК к обоим концам двухцепочечной молекулы. Таким образом можно конструировать произвольную цепь ДНК (рис. 3).
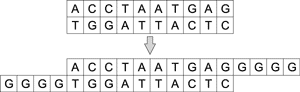
Рис. 3. Процесс удлинения цепочки ДНК
За укорачивание и разрезание молекул ДНК отвечают ферменты — нуклеазы. Различают эндонуклеазы и экзонуклеазы. Последние могут укорачивать и одноцепочечные и двухцепочечные молекулы с одного или с обоих концов (рис. 4), а эндонуклеазы — только с концов.
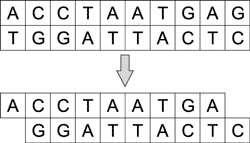
Рис. 4. Процесс укорачивания молекулы
ДНК под воздействием экзонуклеазы
Разрезание молекул ДНК возможно под воздействием сайт-специфичных эндонуклеазов — рестриктазов, которые разрезают их в определенном месте, закодированном последовательностью нуклеотидов (сайтом узнавания). Разрез может быть прямым или несимметричным и проходить по сайту узнавания либо вне его. Эндонуклеазы разрушают внутренние связи в молекуле ДНК (рис. 5).
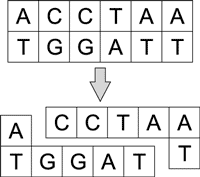
Рис. 5. Разрезание молекулы ДНК
под воздействием рестриктазов
Сшивка — операция, обратная разрезанию, — происходит под воздействием ферментов — лигазов. «Липкие концы» соединяются вместе с образованием водородных связей. Лигазы служат для того, чтобы закрыть насечки, то есть способствовать образованию в нужных местах фосфодиэфирных связей, соединяющих основания друг с другом в пределах одной цепочки (рис. 6).
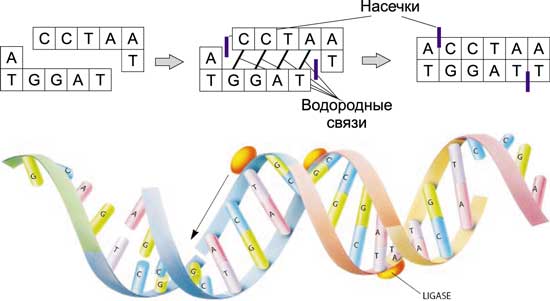
Рис. 6. Сшивка ДНК-молекул под воздействием лигазов
Еще одна интересная операция над ДНК-молекулами, которую можно отнести к числу базовых, — это модификация. Она используется для того, чтобы рестриктазы не смогли найти определенный сайт и не разрушили молекулу. Существует несколько типов модифицирующих ферментов — метилазы, фосфатазы и т.д.
Метилаза имеет тот же сайт узнавания, что и соответствующая рестриктаза. При нахождении нужной молекулы метилаза модифицирует участок с сайтом так, что рестриктаза уже не сможет идентифицировать эту молекулу.
Копирование, или размножение, ДНК-молекул осуществляется в ходе полимеразной цепной реакции (Polymerase Chain Reaction, PCR) — рис. 7. Процесс копирования можно разделить на несколько стадий: денатурация, праймирование и удлинение. Он происходит лавинообразно. На первом шаге из одной молекулы образуются две, на втором — из двух молекул — четыре, а после n-шагов получается уже 2n молекул.
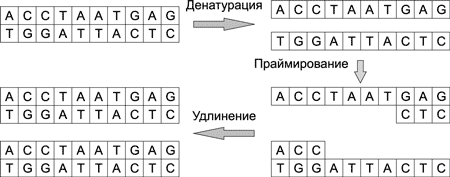
Рис. 7. Процесс копирования ДНК-молекулы
Еще одна операция, которую можно производить над ДНК-молекулами, — это секвенирование, то есть определение последовательности нуклеотидов в ДНК. Для секвенирования цепочек разной длины применяют различные методы. При помощи метода праймер-опосредованной прогулки удается на одном шаге секвенировать последовательность в 250-350 нуклеотидов. После открытия рестриктаз стало возможным секвенировать длинные последовательности по частям.
Ну и последняя процедура, которую мы упомянем, — это гель-электрофорез, используемый для разделения молекул ДНК по длине. Если молекулы поместить в гель и приложить постоянное электрическое поле, то они будут двигаться по направлению к аноду, причем более короткие молекулы будут двигаться быстрее. Используя данное явление, можно реализовать сортировку ДНК-молекул по длине.
ДНК-вычисления
ДНК-молекулы со своей уникальной формой строения и возможностью реализовать параллельные вычисления позволяют по-другому взглянуть на проблему компьютерных вычислений. Традиционные процессоры выполняют программы последовательно. Несмотря на существование многопроцессорных систем, многоядерных процессоров и различных технологий, направленных на повышение уровня параллелизма, в своей основе все компьютеры, построенные на основе фон-неймановской архитектуры, являются устройствами с последовательным режимом выполнения команд. Все современные процессоры реализуют следующий алгоритм обработки команд и данных: выборка команд и данных из памяти и исполнение инструкций над выбранными данными. Этот цикл повторяется многократно и с огромной скоростью.
ДНК-вычисления имеют в своей основе абсолютно иную, параллельную архитектуру и в ряде случаев именно благодаря этому способны с легкостью рассчитывать те задачи, для решения которых компьютерам на базе фон-неймановской архитектуры потребовались бы годы.
Эксперимент Эдлмана
История ДНК-вычислений начинается в 1994 году. Именно тогда Леонард М. Эдлман (Leonard M. Adleman) попытался решить весьма тривиальную математическую задачу абсолютно нетривиальным способом — с использованием ДНК-вычислений. Фактически это было первой демонстраций прототипа биологического компьютера на основе ДНК-вычислений.
Задача, которую Эдлман выбрал для выполнения с помощью ДНК-вычислений, известна как поиск гамильтонова пути в графе или выбор маршрута путешествия (traveling salesman problem). Смысл ее заключается в следующем: имеется несколько городов, которые необходимо посетить, причем побывать в каждом городе можно только один раз.
Зная пункт отправления и конечный пункт, необходимо определить маршрут путешествия (если он существует). При этом маршрут составляется с учетом возможных авиаперелетов и коннектов различных авиарейсов.
Итак, предположим, что имеется всего четыре города (в эксперименте Эдлмана использовалось семь городов): Атланта (Atlanta), Бостон (Boston), Детройт (Detroit) и Чикаго (Chicago). Перед путешественником ставится задача выбрать маршрут, чтобы попасть из Атланты в Детройт, побывав при этом в каждом городе только один раз. Схемы возможных сообщений между городами показаны на рис. 8.
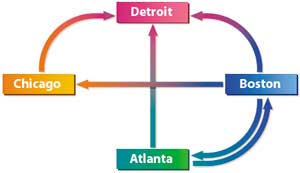
Рис. 8. Схемы возможных сообщений
между городами
Нетрудно заметить (для этого требуется всего несколько секунд), что единственно возможный маршрут (гамильтонов путь) следующий: Атланта — Бостон — Чикаго — Детройт.
Действительно, при небольшом количестве городов составить такой маршрут довольно просто. Но с увеличением их числа сложность решения задачи экспоненциально возрастает и становится трудновыполнимой не только для человека, но и для компьютера.
Так, на рис. 9 показан граф из семи вершин с указанием возможных переходов между ними. Для поиска гамильтонова пути обычному человеку требуется не более одной минуты. Именно такой граф был использован в эксперименте Эдлмана. На рис. 10 представлен граф из 12 вершин — в этом случае поиск гамильтонова пути оказывается уже не такой простой задачей. Вообще, сложность решения задачи поиска гамильтонова пути возрастает экспоненциально с ростом числа вершин в графе. К примеру, для графа из 10 вершин существует 106 возможных путей; для графа из 20 вершин — 1012, а для графа из 100 вершин — 10100 вариантов. Понятно, что в последнем случае для генерации всех возможных путей и их проверки потребуется огромное время даже для современного суперкомпьютера.
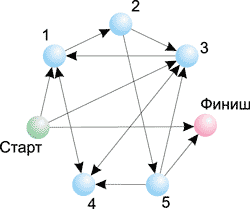
Рис. 9. Поиск оптимального маршрута путешествия
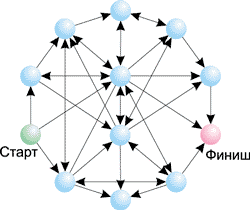
Рис. 10. Граф, состоящий из 12 вершин
Итак, вернемся к нашему примеру с поиском гамильтонова пути в случае четырех городов (см. рис. 8).
Для решения данной задачи с использованием ДНК-вычислений Эдлман закодировал название каждого города в виде одной цепочки ДНК, причем каждая из них содержала 20 базовых оснований. Для простоты мы будем кодировать каждый город ДНК-цепочкой из восьми оснований. ДНК-коды городов показаны в табл. 1. Обратите внимание, что цепочка длиной в восемь базовых оснований оказывается избыточной для кодирования всего четырех городов.
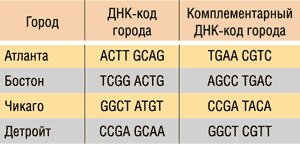
Таблица 1. ДНК-коды городов
Отметим, что для каждого ДНК-кода города, который определяет одинарную ДНК-цепочку, существует и комплементарная цепочка, то есть комплементарный ДНК-код города, причем и ДНК-код города, и комплементраный код абсолютно равноправны.
Далее с помощью одинарных ДНК-цепочек необходимо закодировать все возможные перелеты (Атланта — Бостон, Бостон — Детройт, Чикаго — Детройт и т.д.). Для этого использовался следующий подход. Из названия города отправления брались четыре последних базовых основания, а из названия города прибытия — четыре первых.
К примеру, перелету Атланта — Бостон будет соответствовать следующая последовательность: GCAG TCGG (рис. 11).
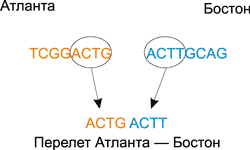
Рис. 11. Кодирование перелетов между городами
ДНК-кодирование всех возможных перелетов показано в табл. 2.
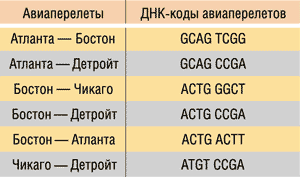
Таблица 2. ДНК-коды всех возможных перелетов
Итак, после того как готовы коды городов и возможных перелетов между ними, можно непосредственно переходить к вычислению гамильтонова пути. Процесс вычисления состоит из четырех этапов:
- Сгенерировать все возможные маршруты.
- Отобрать маршруты, которые начинаются в Атланте и заканчиваются Детройтом.
- Выбрать маршруты, длина которых соответствует количеству городов (в нашем случае длина маршрута составляет четыре города).
- Выбрать маршруты, в которых каждый город присутствует только один раз.
Итак, на первом этапе мы должны сгенерировать все возможные маршруты. Напомним, что правильный маршрут соответствует перелетам Атланта — Бостон — Чикаго — Детройт. Этому маршруту соответствует ДНК-молекула GCAG TCGG ACTG GGCT ATGT CCGA.
Для того чтобы сгенерировать все возможные маршруты достаточно поместить в пробирку все необходимые и заранее заготовленные ингредиенты, то есть ДНК-молекулы, соответствующие всем возможным перелетам, и ДНК-молекулы, соответствующие всем городам. Но вместо того, чтобы применять одинарные ДНК-цепочки, соответствующие названиям городов, необходимо использовать комплементарные им ДНК-цепочки, то есть вместо ДНК-цепочки ACTT GCAG, соответствующей Атланте, будем применять комплементарную ДНК-цепочку TGAA CGTC и т.д., поскольку ДНК-код города и комплементраный код абсолютно равноправны.
Далее все эти молекулы (достаточно буквально щепотки, которая будет содержать порядка 1014 различных молекул) помещаем в воду, добавляем лигазов, произносим заклинание и… буквально через несколько секунд получаем все возможные маршруты.
Процесс образования цепочек ДНК, соответствующих различным маршрутам, происходит следующим образом. Рассмотрим, к примеру, цепочку GCAG TCGG, отвечающую за перелет Атланта — Бостон. Вследствие высокой концентрации различных молекул, данная цепочка обязательно встретится с комплементарной ДНК-цепочкой AGCC TGAC, соответствующей Бостону. Поскольку группы TCGG и AGCC комплементарны друг другу, то за счет образования водородных связей эти цепочки сцепятся друг с другом (рис. 12).
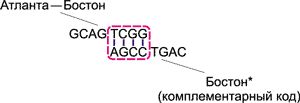
Рис. 12. Сцепление цепочек, соответствующих
перелету Атланта — Бостон и Бостону
Теперь образовавшаяся цепочка неминуемо встретится с ДНК-цепочкой ACTG GGCT, соответствующей авиаперелету Бостон — Чикаго, и поскольку группа ACTG (первые четыре основания в этой цепочке) комплементарна группе TGAC (последние четыре основания в комплементарном коде Бостона), то ДНК-цепочка ACTG GGCT присоединится к уже образовавшейся цепочке. Далее к этой цепочке таким же образом присоединится ДНК-цепочка, соответствующая городу Чикаго (комплементарный код), а затем и цепочка авиаперелета Чикаго — Детройт. Процесс образования маршрута показан на рис. 13.
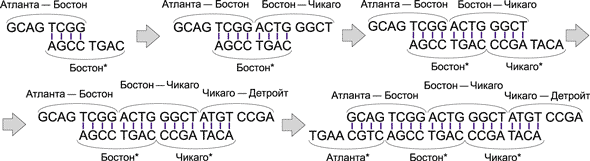
Рис. 13. Процесс образования ДНК-цепочки, соответствующей маршруту
Атланта — Бостон — Чикаго — Детройт
Мы рассмотрели пример образования только одного маршрута (причем это именно гамильтонов маршрут). Аналогичным образом получаются и все остальные возможные маршруты (например, Атланта — Бостон — Атланта — Детройт). Важно, что все маршруты формируются одновременно, то есть параллельно. Причем время, требуемое для создания всех возможных маршрутов в данной задаче и всех маршрутов в задаче с 10 или 20 городами, абсолютно одинаково (лишь бы хватило исходных ДНК-молекул). Собственно, именно в параллельном алгоритме ДНК-вычислений и заключается основное преимущество в сравнении с фон-неймановской архитектурой.
Итак, в пробирке образованы ДНК-молекулы, соответствующие всем возможным маршрутам. Однако это еще не решение задачи — нам необходимо выделить ту единственную ДНК-молекулу, которая отвечает за гамильтонов маршрут. Поэтому на следующем этапе необходимо отобрать молекулы, соответствующие маршрутам, начинающимся в Атланте и заканчивающимся в Детройте.
Для этого используется полимеразная цепная реакция (PCR), в результате которой создается множество копий только тех ДНК-цепочек, которые начинаются с кода Атланты и заканчиваются кодом Детройта.
Для реализации полимеразной цепной реакции применяются два прайма: GCAG и GGCT. Процесс копирования ДНК-модекул, начинающихся с ДНК-кода Атланты и заканчивающихся ДНК-кодом Детройта, показан на рис. 14.
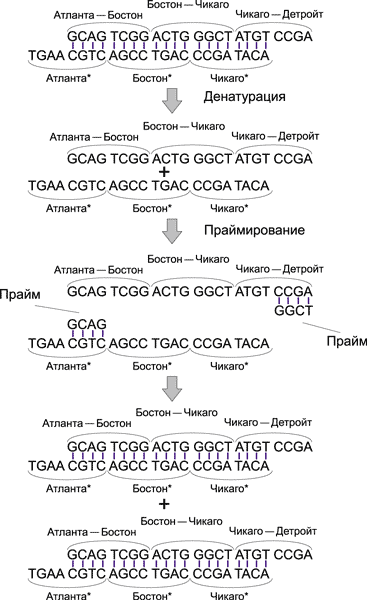
Рис. 14. Процесс копирования ДНК-молекул в ходе PCR-реакции
Отметим, что в присутствии праймов GCAG и GGCT будут копироваться и те ДНК-молекулы, которые начинаются с ДНК-кодов Атланты, но не заканчиваются ДНК-кодом Детройта (под действием прайма GCAG), а также ДНК-молекулы, которые заканчиваются ДНК-кодом Детройта, но не начинаются с ДНК-кода Атланты (под действием прайма GGCT). Понятно, что скорость копирования таких молекул будет гораздо ниже скорости копирования ДНК-молекул, начинающихся с ДНК-кода Атланты и заканчивающихся ДНК-кодом Детройта. Следовательно, после PCR-реакции мы получим преобладающее количество ДНК-молекул в форме регулярной двойной спирали, соответствующих маршрутам, начинающимся в Атланте и заканчивающимся в Детройте.
На следующем этапе необходимо выделить молекулы нужной длины, то есть те, что содержат ДНК-коды ровно четырех городов. Для этого используется гель-электрофорез, что позволяет отсортировать молекулы по длине. В результате мы получаем молекулы нужной длины (ровно четыре города), начинающиеся с кода Атланты и заканчивающиеся кодом Детройта.
Теперь необходимо убедиться, что в отобранных молекулах код каждого города присутствует только один раз. Эта операция реализуется с применением процесса, известного как affinity purification.
Для данной операции используется микроскопический магнитный шарик диаметром порядка одного микрона. К нему притягиваются комлементарные ДНК-коды того или иного города, которые выполняют функцию пробы. К примеру, если требуется проверить, присутствует ли в исследуемой ДНК-цепочке код города Бостона, то необходимо сначала поместить магнитный шарик в пробирку с ДНК-молекулами, соответствующими ДНК-кодам Бостона. В результате мы получим магнитный шарик, облепленный нужными нам пробами. Затем этот шарик помещается в пробирку с исследуемыми ДНК-цепочками — в результате к нему (за счет образования водородных связей между комплементарными группами) притянутся ДНК-цепочки, в которых присутствует комплементарный код Бостона. Далее шарик с отсортированными молекулами вынимается и помещается в новый раствор, из которого затем удаляется (при повышении температуры ДНК-молекулы отваливаются от шарика). Данная процедура (сортировка) повторяется последовательно для каждого города, и в результате мы получаем только те молекулы, в которых содержатся ДНК-коды всех городов, а значит, и маршруты, соответствующие гамильтонову пути. Фактически задача решена — осталось лишь просчитать ответ.
Заключение
Эдлман продемонстрировал решение задачи поиска гамильтонова пути на примере всего семи городов и потратил на это семь дней. Это был первый эксперимент, продемонстрировавший возможности ДНК-вычислений. Фактически Эдлман доказал, что, пользуясь вычислениями на ДНК, можно эффективно решать задачи переборного характера, и обозначил технику, которая в дальнейшем послужила основой для создания модели параллельной фильтрации.
Впрочем, многие исследователи не испытывают оптимизма по поводу будущего биологических компьютеров. Вот лишь маленький пример. Если бы подобным методом понадобилось найти гамильтонов путь в графе, состоящем из 200 вершин, потребовалось бы количество ДНК-молекул, сопоставимое по весу со всей нашей планетой! Это принципиальное ограничение, конечно же, является своего рода тупиковой ситуацией. Поэтому многие исследовательские лаборатории (например, компания IBM) предпочли сфокусировать свое внимание на других идеях альтернативных компьютеров, таких как углеродные нанотрубки и квантовые компьютеры.
После эксперимента Эдлмана было проведено множество других исследований возможностей ДНК-вычислений. Например, можно вспомнить опыт Э.Шапиро: в нем был реализован конечный автомат, который может находиться в двух состояниях: S0 и S1 — и отвечает на вопрос: четное или нечетное количество символов содержится во входной последовательности символов.
Сегодня ДНК-вычисления — это не более чем перспективные технологии на уровне лабораторных исследований, причем в таком состоянии они будут находиться еще не один год. Фактически на современном этапе развития необходимо ответить на следующий глобальный вопрос: какой класс задач поддается решению при помощи ДНК и можно ли построить общую модель ДНК-вычислений, пригодную как для реализации, так и для использования?








