Flash-код и красота формул
Flash-композиции на основе спирали
Красота — это бесконечность,
выраженная в законченной форме.
Фридрих Шеллинг
Пионеры компьютерной живописи имели в своем распоряжении весьма ограниченный набор программ для создания графики. Компьютерным художником мог быть только программист-математик, способный написать код и отобразить его в графическом виде на экране. За последние же двадцать лет появилось столько специализированных программ, позволяющих создавать изображения, не написав ни строчки кода и не задумываясь о том, какая математика стоит за той или иной совокупностью линий, что, казалось бы, рисовать картины посредством программирования никто не захочет. Однако это не так. Сегодня немало художников, которые создают компьютерные произведения именно путем написания кода. Они называют себя приверженцами направлений Algorithmic art, Equation art, Fractal art и охотно размещают свои творения в Сети.
Термин « алгоритмируемое искусство» (Algorithmic art или Algorithm art), появившийся в начале 60-х годов, относится к произведениям, которые генерируются компьютером по некоему алгоритму, заложенному автором. Считается, что первыми в стиле Algorithmic art начали творить Георг Ни (Georg Nees), Фрайдер Нейк (Frieder Nake) и Герберт Франк (Herbert W. Franke), работы которых были выполнены на базе плоттера, управляемого компьютером, и первых черно-белых экранов. Их композиции (рис. 1 и 2) стали, что называется, классикой жанра, а скачать их в высоком разрешении можно, например, по адресу: http://www.abteiberginfo.de.
Рис. 1. Георг Ни. Siemenssystem 4004. Начало 60-х годов

Рис. 2. Герберт Франк. 1961/62
Частными случаями Algorithm ic art являются фрактальное искусство (Fractal art) и уже упомянутое Equation art (дословно — произведение на основе уравнения). Термин «фрактальное искусство»1 появился в начале 80-х годов, а понятие «Equation art» — сравнительно недавно, в 2000 году. Представители последнего направления подчеркивают, что алгоритм, реализующий произведение, базируется не на случайных процессах, а задается уравнениями, которые автор закладывает в основу своей композиции. Творческая задача художника, создающего подобную графику, состоит в нахождении (написании) уравнения, которое формирует визуально интересный результат, а мастерство выражается в способности представить математически те визуальные композиции, которые рождает воображение художника.
Работы в стиле Equation art можно посмотреть на сайте одного из идеологов этого направления Патрика Хедлеса (Patrick Heddles) по адресу: http://www.pheddles.com/gallery.php?offset=84&width=1152&height=864 (рис. 3).
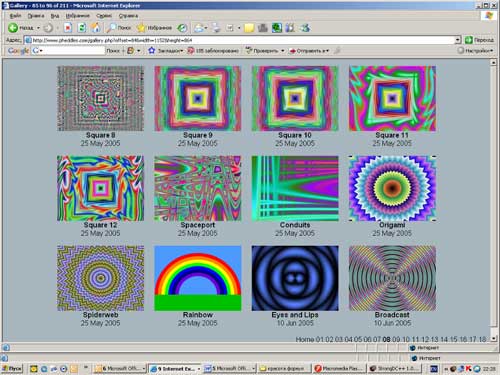
Рис. 3. Сайт Патрика Хедлеса
Зачастую удачное название композиции, как и в абстрактной живописи, усиливает эффект восприятия. Например, работы «Широковещание» и «Глаза и губы» Хедлеса запоминаются именно благодаря своим метким названиям, как нельзя лучше раскрывающим суть образов.
В стиле Equation art работает также Ричард Грантхем (Richard Grantham), работы которого можно увидеть по адресу: http://www.anagrammy.com/applets/grampicapplet.html (рис. 4). Причем в Сети можно найти не только его графику, но и строчки кода, порождающие данные изображения.
Рис. 4. Ричард Грантхем. Анаграммы
В этом же стиле создает картины Карпи Корнер ( Karpie' s Korner) — его произведения можно посмотреть по адресу: http://karpie.net/gallery.php?offset=0 (рис. 5 и 6).

Рис. 5. Карпи Корнер. Голубое никуда ( Blue Nowhere ). 2005

Рис. 6. Карпи Корнер. Лотос ( Lotus ). 2005
Особенностью Algorithmic art является то, чтохудожник сам пишет код, а не пользуется чужим программным продуктом, который автоматически генерирует образы. Таким образом, если пользователь создает компьютерную графику с помощью какой-либо программы, например Adobe Photoshop, и работает компьютерной кистью, то его произведения не относятся к направлению Algorithmic art , несмотря на то, что программа Photoshop интегрирует в себе десятки алгоритмов и сотни строчек кода.
Не углубляясь в эстетический аспект данной «формульной живописи», следует отметить, что умение увидеть за графическим образом его математическое выражение, несомненно, способствует развитию математического мышления и навыков программирования. Подобные творческие эксперименты независимо от эстетической ценности генерируемых произведений полезны для школьников и студентов, изучающих информатику и, в особенности, компьютерную графику.
Именно это побудило автора рассмотреть создание изображений в стиле Algorithmic art на базе программы Flash. На наш взгляд, в данном отношении Flash является уникальным средством. Программа предоставляет пользователю не только привычные инструменты (карандаш, кисть и т.п.) и возможность написания довольно сложного ActionScript-кода, но и комбинированный подход — дублирование и трансформацию рисованных объектов путем написания кода.
Более того, Flash, будучи разработанной специально для анимации, позволяет легко создавать динамические композиции, которые иногда называют Algorithmic video. В данной статье мы приводим не только работы художников, работающих в стиле Equation art, но и некоторые результаты собственных экспериментов по написанию Flash-кода для создания визуально интересных композиций. На прилагаемом к журналу CD-диске можно найти описываемые в статье ролики, а также исходные FLA-файлы, так что читатели могут не только посмотреть наши работы, но и поэкспериментировать с ними, меняя коэффициенты в формулах.
Возможно, статья сподвигнет кого-то на создание собственных композиций в этом стиле. Присылайте свои работы к нам в редакцию. Наиболее интересные из них мы с удовольствием опубликуем на нашем диске и расскажем об авторах.
Flash-композиции на основе спирали
Чтобы создать картинку в стиле Algorithm art, в качестве базового мы выбрали уравнение спирали и сгенерировали на его основе различные динамические композиции (рис. 7). Выбор был не случайным — в самом уравнении спирали скрыта своеобразная красота.

Рис. 7. Спиралевидные по форме галактика, раковина улитки, а также Flash-композиции
Еще великий Гете подчеркивал особую роль спирали в природе и называл ее «кривой жизни». Спиралью завивается раковина улитки, спиралевидно располагаются листья на ветках деревьев, семена в подсолнечнике и шишках сосны, паук плетет спиралевидную паутину, спиралью закручивается ураган, испуганное стадо северных оленей разбегается по спирали, молекула ДНК закручена двойной спиралью, форму спирали имеют далекие галактики.
С математической точки зрения спираль — это кривая, которая огибает некоторую центральную точку или ось, постепенно приближаясь или удаляясь от нее, в зависимости от направления обхода кривой.
Если начало спирали принять за полюс полярной системы координат, то математически спираль может быть представлена с помощью некоторого полярного уравнения ρ = f(j), где ρ — радиус-вектор спирали, j — угол, откладываемый на полярной оси, f(j) — некоторая монотонно возрастающая или убывающая положительная функция.
Мы рассматривали две спирали: логарифмическую (рис. 8) и спираль Архимеда.
Логарифмическая спираль в полярных координатах (ρ, ![]() ) может быть описана формулой:
) может быть описана формулой:
ρ = keb![]() .
.

Рис. 8. Логарифмическая спираль
Особый интерес представляет так называемая золотая спираль. Как известно, золотое сечение (золотая пропорция) — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как большая часть относится к меньшей. Золотым прямоугольником называется прямоугольник, в котором отношение большей стороны к меньшей равно золотой пропорции. Такой прямоугольник можно использовать для построения золотой спирали. Любой золотой прямоугольник можно разделить на квадрат и меньший золотой прямоугольник (рис. 9). Теоретически этот процесс можно продолжать до бесконечности (получаются прямоугольники A, B, C, D, E, F, G и т.д.) Пунктирные линии, которые сами находятся в золотом соотношении одна к другой, рассекают прямоугольники по диагонали и обозначают теоретический центр спирали. В любой точке развития золотой спирали отношение длины дуги к ее диаметру равно 1,618.
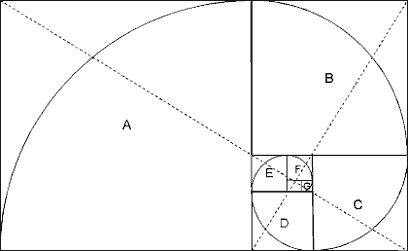
Рис. 9. Построение золотой спирали
Очень многие явления в природе описываются именно золотой спиралью. Расположение космических галактик, семян в шишке, завитков в раковине и многого другого подчинено закону золотой спирали. «Вечность времени и световые годы космоса разделяют сосновую шишку и спиральную галактику, но строение остается тем же самым: коэффициент 1,618, возможно, первостепенный закон, управляющий активными природными явлениями. Таким образом, золотая спираль развертывается перед нами в символической форме, как один из величественных замыслов природы, образ жизни в бесконечном расширении и сжатии, статический закон, управляющий динамическим процессом, подкрепленный и изнутри и снаружи пропорцией 1,618, золотым сечением»2.

Рис. 10. Расположение тычинок в точности описывается золотой спиралью
В первой композиции мы просто решили выложить логарифмическую спираль шариками.
Рис. 11. Исходное изображение
Для того чтобы исходный мувиклип (шарик) на рис. 11 не мешал композиции, мы поместили его за границу сцены, присвоили экземпляру имя mc и на первый кадр поместили следующий код:
N_rot = 600; // количество дублируемых элементов
b = 0.2; // коэффициент в показателе степени
dfi=0.1; // шаг приращения угла
k=0.5; // коэффициент перед экспонентой
fi= 0; // начальное значение угла
for (i=1; i<=N_rot; i++) {
fi = fi + dfi;
pokaz =b*fi;
ro = k * Math.pow(Math.E, pokaz);
mc.duplicateMovieClip ("mc"+i, i);
this["mc"+i]._x = ro* Math.sin(fi) +400;
this["mc"+i]._y = ro* Math.cos(fi) +400;
}
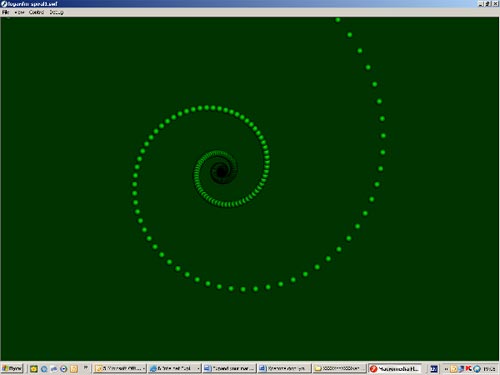
Рис. 12. Логарифмическая спираль (статическая картинка)
В результате мы получили статическую картинку (рис. 12). Далее мы ввели цикл по кадрам, меняя шаг приращения угла, варьируя коэффициенты и уменьшая размер шариков по мере их приближения к центру.
N_rot = 600
b = 0.2
dfi=0.1
k=0.5
_root.onEnterFrame = function (){
fi= 0
k= k+0.3
dfi= dfi+0.001
for (i=1; i<=N_rot; i++) {
fi = fi + dfi;
pokaz =b*fi;
ro = k * Math.pow(Math.E, pokaz);
mc.duplicateMovieClip ("mc"+i, i);
this["mc"+i]._x = ro* Math.sin(fi) +400;
this["mc"+i]._y = ro* Math.cos(fi) +400;
this["mc"+i]._xscale = fi*3;
this["mc"+i]._yscale = fi*3;
}
}
В результате получилась динамическая картинка разворачивающейся спирали (рис. 13).
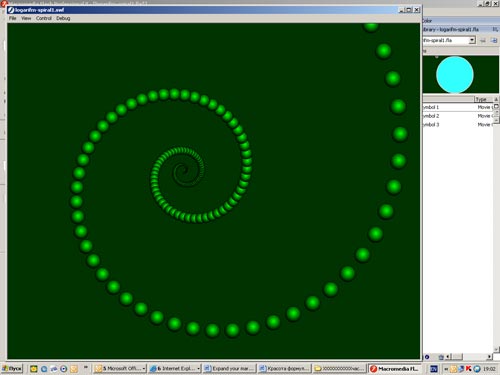
Рис. 13. Один из кадров ролика с разворачивающейся спиралью
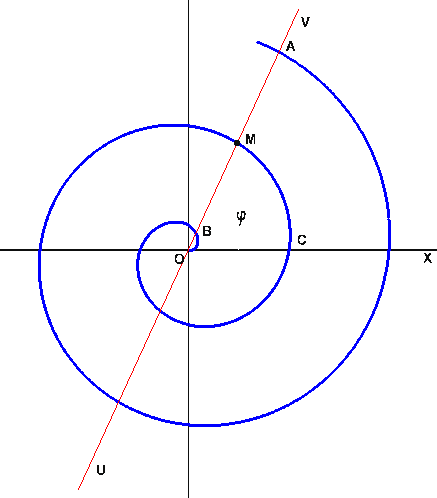
Более интересные композиции удалось получить на базе уравнения спирали Архимеда, в которой увеличение шага равномерно. Такие спирали распространены в природе и широко применяются в технике (рис. 14).
Расстояние ρ = OM пропорционально углу поворота ![]() луча OV. Повороту луча OV на один и тот же угол соответствует одно и то же приращение ρ.
луча OV. Повороту луча OV на один и тот же угол соответствует одно и то же приращение ρ.
Уравнение спирали Архимеда в полярной системе координат записывается следующим образом:
ρ = k![]() ,
,
где k — смещение точки M по лучу r при повороте на угол, равный одному радиану.
Повороту прямой на 2![]() соответствует смещение a = |BM| = |MA| = 2k
соответствует смещение a = |BM| = |MA| = 2k![]() . Число a называется шагом спирали. Уравнение спирали Архимеда можно переписать так:
. Число a называется шагом спирали. Уравнение спирали Архимеда можно переписать так:
![]()
Рис. 14. Спираль Архимеда
Нижеследующий код создает ряд непрерывно меняющихся динамических картин, одна из которых показана на рис. 15.
N_rot = 360
dfi=0.1
_root.onEnterFrame = function (){
fi= 0
dfi = dfi+ 0.005
k= 1.5
for (i=1; i<=N_rot; i++) {
fi = fi + dfi;
ro = k * fi;
mc.duplicateMovieClip ("mc"+i, i);
this["mc"+i]._x = ro* Math.sin(fi) +400;
this["mc"+i]._y = ro* Math.cos(fi) +400;
this["mc"+i]._xscale = 20 + fi/3;
this["mc"+i]._yscale = 20 + fi/3;
}
}

Рис. 15. Один из кадров ролика, построенного на базе уравнения спирали Архимеда
Варьируя исходный мувиклип и меняя характер изменения приращения угла, можно получить весьма необычные картинки (рис. 16).

Рис. 16. Изображение, полученное при неравномерном приращении угла
Рис. 17 был создан в результате усложнения исходного мувиклипа: мы наложили друг на друга четыре шарика разных диаметров и цветов.

Рис. 17. Два кадра из одного ролика с наложением шариков разных цветов
Программа Flash позволяет создавать рисунок, располагая на плоскости нарисованные от руки предметы согласно некоторому уравнению. На рис. 18 показана картинка, полученная с помощью того же кода, но вместо дублируемого мувиклипа в виде шарика использовалось растровое изображение кристалла.

Рис. 18. В качестве исходного изображения использован растровый рисунок
Аналогично для получения картинки, представленной на рис. 19, применялось изображение кленового листа. При этом в программу была добавлена строчка, которая задает поворот листьев вокруг собственной оси.

Рис. 19. Композиция «Листопад»: кленовые листья кружатся, двигаясь по спирали
Отнюдь не претендуя на эстетическую ценность наших композиций, отметим, что в них проявляется красота спирали.
Кстати, понятие «красота формулы» недавно получило еще одну интересную трактовку. Ученые из Калифорнийского университета, выполнив ряд экспериментов, смогли доказать, что человек считает образ или предмет более или менее красивым в зависимости от того, насколько быстро его мозг способен обработать данное изображение. Петр Винкельман, профессор из Калифорнийского университета, отмечает: «Стремление мозга к экономии энергии объясняет культурные и исторические отличия в восприятии красоты. Человеку кажется красивым то, что более привычно и что легче воспринимается». Недаром великие художники соблюдали пропорции золотого сечения и золотой спирали в своих полотнах (рис. 20).

Рис. 20. Золотая спираль в картине Рафаэля «Избиение младенцев»
Для тех, кому эксперименты ради экспериментов кажутся занятием малополезным, заметим, что подобным рисункам можно найти и практическое применение.
Несложно написать программку, генерирующую регулярные узоры (такие, например, как на рис. 21), на базе которых можно создавать узоры для тканей, обоев и т.п.

Рис. 21. Регулярный узор на основе спирали
При рассмотрении спиралевидных изображений у автора возникла еще одна идея: использовать представление иконок графических файлов в виде спирали во вьюерах, что обеспечит быстрый доступ к большему количеству снимков. Например, на рис. 22 слева расположено 60 иконок фотографий, а справа — всего 25.

Рис. 22. Расположение иконок по спирали обеспечивает быстрый доступ к большему количеству изображений
Фотографии часто снимаются сериями с одним и тем же фоном (например «дома», «на даче», «на дне рождения» и т.п.), поэтому при расположении миниатюр в форме спирали можно увидеть ту или иную серию даже на мелких перекрывающиеся фото.
Несложно создать в подобном вьюере функцию, чтобы по щелчку мыши какую-либо серию фотографий можно было перевести на более широкий виток спирали и рассмотреть при большем разрешении или увеличить до большого размера отдельное фото. В спираль можно уложить любое количество фотографий. Здесь, как на грампластинке, имеющей спиралевидную канавку, возможен мгновенный доступ к любому фрагменту информации.
При этом спирали не обязательно быть круговой, она может иметь прямоугольную форму — в этом случае пространство будет использоваться более экономно.
Такая форма представления материалов удобна и при отображении файловой структуры и т.п.
Авторы будут признательны за комментарии, которые можно присылать по адресу: alproh@ aha. ru.
1Тема фрактального искусства настолько широка, что о ней хотелось бы рассказать в отдельной статье.
2Frost A.J., Prechter R.Jr. Под общ. ред. И.О. Закарян, пер. Д. Ввозного // http://www.alpari-idc.ru/ru/textbook/tech_an/ew/17.php.