Квантовый компьютер

Сергей Пахомов

Ограниченные возможности современных компьютеров

Квантовая физика

Появление квантовых вычислений

Идея квантовых вычислений

Структура квантового компьютера

Практическое применение квантовых компьютеров

Еще пять лет назад о квантовых компьютерах знали разве что специалисты в области квантовой физики. Однако в последние годы количество публикаций в Интернете и в специализированных изданиях, посвященных квантовым вычислениям, возрастало лавинообразно. Тема квантовых вычислений стала популярной и вызвала множество различных мнений, далеко не всегда соответствующих действительности.
В настоящей статье мы постараемся как можно более доступно рассказать о том, что же такое квантовый компьютер и на какой стадии находятся современные разработки в этой области.

Ограниченные возможности современных компьютеров

О квантовых компьютерах и квантовых вычислениях часто говорят как об альтернативе кремниевым технологиям создания микропроцессоров, что, в общем-то, не совсем верно. Собственно, почему вообще приходится искать альтернативу современным компьютерным технологиям? Как показывает вся история существования компьютерной индустрии, вычислительная мощность процессоров возрастает экспоненциально. Ни одна другая индустрия не развивается столь бурными темпами. Как правило, когда говорят о темпах роста вычислительной мощности процессоров, вспоминают так называемый закон Гордона Мура, выведенный в апреле 1965 года, то есть всего через шесть лет после изобретения первой интегральной схемы (ИС).

По просьбе журнала «Электроникс» (“Electronics”) Гордон Мур написал статью, приуроченную к 35-й годовщине издания. Он сделал прогноз относительно того, как будут развиваться полупроводниковые устройства в течение ближайших десяти лет. Проанализировав темпы развития полупроводниковых устройств и экономические факторы за прошедшие шесть лет, то есть начиная с 1959 года, Гордон Мур предположил, что к 1975 году количество транзисторов в одной интегральной микросхеме составит 65 тыс.

Фактически по прогнозу Мура количество транзисторов в одной микросхеме за десять лет должно было увеличиться более чем в тысячу раз. В то же время это означало, что каждый год количество транзисторов в одной микросхеме должно удваиваться.

Впоследствии в закон Мура были внесены коррективы (дабы соотнести его с реальностью), но смысл от этого не поменялся: количество транзисторов в микросхемах увеличивается экспоненциально. Естественно, увеличение плотности размещения транзисторов на кристалле возможно лишь за счет сокращения размеров самих транзисторов. В связи с этим уместен вопрос: до какой степени можно уменьшать размеры транзисторов? Уже сейчас размеры отдельных элементов транзисторов в процессорах сопоставимы с атомарными, например ширина диоксидного слоя, отделяющего диэлектрик затвора от канала переноса заряда, составляет всего несколько десятков атомарных слоев. Понятно, что существует чисто физический предел, делающий невозможным дальнейшее уменьшение размеров транзисторов. Даже если предположить, что в будущем они будут иметь несколько иную геометрию и архитектуру, теоретически невозможно создать транзистор или подобный ему элемент с размером менее 10^-8 см (диаметр атома водорода) и рабочей частотой более 10¹⁵ Гц (частота атомных переходов). А потому, хотим мы того или нет, неизбежен тот день, когда закон Мура придется сдать в архив (если, конечно, его в очередной раз не подкорректируют).

Ограниченные возможности по наращиванию вычислительной мощности процессоров за счет сокращения размеров транзисторов — это лишь одно из узких мест классических кремниевых процессоров.

Как мы увидим в дальнейшем, квантовые компьютеры никоим образом не представляют собой попытку решения проблемы миниатюризации базовых элементов процессоров.

Решение проблемы миниатюризации транзисторов, поиск новых материалов для создания элементной базы микроэлектроники, поиск новых физических принципов для приборов с характерными размерами, сравнимыми с длиной волны Де-Бройля, имеющей величину порядка 20 нм, — эти вопросы стоят на повестке дня уже почти два десятилетия. В результате их решения была разработана нанотехнология. Серьезной проблемой, с которой пришлось столкнуться при переходе в область наноэлектронных устройств, является уменьшение рассеиваемой энергии в процессе вычислительных операций. Мысль о возможности «логически обратимых» операций, не сопровождающихся рассеянием энергии, впервые высказал Р.Ландауер еще в 1961 году. Существенный шаг в решении данной задачи был сделан в 1982 году Ч.Беннеттом, который теоретически доказал, что универсальный цифровой компьютер может быть построен на логически и термодинамически обратимых вентилях таким образом, что энергия будет рассеиваться только за счет необратимых периферийных процессов ввода информации в машину (приготовление исходного состояния) и соответственно вывода из нее (считывание результата). К типичным обратимым универсальным вентилям относятся вентили Фредкина и Тоффоли.

Другая проблема, связанная с классическими компьютерами, кроется в самой фон-неймановской архитектуре и двоичной логике всех современных процессоров. Все компьютеры, начиная с аналитической машины Чарльза Бэббиджа и заканчивая современными суперкомпьютерами, основаны на одних и тех же принципах (фон-неймановская архитектура), которые были разработаны еще в 40-х годах прошлого столетия.

Любой компьютер на программном уровне оперирует битами (переменными, принимающими значение 0 или 1). С применением логических элементов-вентилей над битами выполняются логические операции, что позволяет получить определенное конечное состояние на выходе. Изменение состояния переменных производится с помощью программы, которая определяет последовательность операций, каждая из которых использует небольшое число бит.

Традиционные процессоры выполняют программы последовательно. Несмотря на существование многопроцессорных систем, многоядерных процессоров и различных технологий, направленных на повышение уровня параллелизма, все компьютеры, построенные на основе фон-неймановской архитектуры, являются устройствами с последовательным режимом выполнения команд. Все современные процессоры реализуют следующий алгоритм обработки команд и данных: выборка команд и данных из памяти и исполнение инструкций над выбранными данными. Этот цикл повторяется многократно и с огромной скоростью.

Однако фон-неймановская архитектура ограничивает возможность увеличения вычислительной мощности современных ПК. Типичный пример задачи, которая оказывается не по силам современным ПК, — это разложение целого числа на простые множители (простым называется множитель, который делится без остатка только на себя и на 1).

Если требуется разложить на простые множители число х, имеющее n знаков в двоичной записи, то очевидный способ решения этой задачи заключается в том, чтобы попробовать последовательно разделить его на числа от 2 до   Для этого придется перебрать 2^n/2 вариантов. К примеру, если рассматривается число, у которого 100 000 знаков (в двоичной записи), то потребуется перебрать 3x10^{15 051}  вариантов. Если предположить, что для одного перебора требуется один процессорный такт, то при скорости в 3 ГГц для перебора всех чисел будет нужно время, превышающее возраст нашей планеты. Существует, правда, хитроумный алгоритм, решающий ту же задачу за exp(n^1/3) шагов, но даже в этом случае с задачей разложения на простые множители числа, имеющего миллион знаков, не справится ни один современный суперкомпьютер.

Задача разложения числа на простые множители относится к классу задач, которые, как говорят, не решаются за полиномиальное время (NP-полная задача — Nondeterministic polynomial-time complete). Такие задачи входят в класс невычисляемых в том смысле, что они не могут быть решены на классических компьютерах за время, полиномиально зависящее от числа битов n, представляющих задачу. Если говорить о разложении числа на простые множители, то по мере увеличения разрядности числа время, необходимое для решения задачи, возрастает экспоненциально, а не полиномиально.

Забегая вперед, отметим, что с квантовыми вычислениями связывают перспективы решения NP-полных задач за полиномиальное время.

Квантовая физика

Конечно, квантовая физика слабо связана с тем, что называют элементной базой современных компьютеров. Однако, говоря о квантовом компьютере, избежать упоминания некоторых специфических терминов квантовой физики просто невозможно. Мы понимаем, что далеко не все изучали легендарный третий том «Теоретической физики» Л.Д.Ландау и Е.М.Лифшица и для многих такие понятия, как волновая функция и уравнение Шредингера, — это что-то из потустороннего мира. Что же касается специфического математического аппарата квантовой механики, то это сплошные формулы и малопонятные слова. Поэтому мы постараемся придерживаться общедоступного уровня изложения, избегая по возможности тензорного анализа и прочей специфики квантовой механики.

Для подавляющего большинства людей квантовая механика находится за гранью понимания. Дело даже не столько в сложном математическом аппарате, сколько в том, что законы квантовой механики нелогичны и не имеют подсознательной ассоциации — их невозможно себе представить. Впрочем, анализ нелогичности квантовой механики и парадоксального рождения из этой нелогичности стройной логики — это удел философов, мы же коснемся аспектов квантовой механики лишь в той мере, в какой это необходимо для понимания сути квантовых вычислений.

История квантовой физики началась 14 декабря 1900 года. Именно в этот день немецкий физик и будущий нобелевский лауреат Макс Планк доложил на заседании Берлинского физического общества о фундаментальном открытии квантовых свойств теплового излучения. Так в физике появилось понятие кванта энергии, а среди других фундаментальных постоянных — постоянная Планка.

Открытие Планка и появившаяся затем, в 1905 году, теория фотоэлектрического эффекта Альберта Эйнштейна, а также создание в 1913 году Нильсом Бором первой квантовой теории атомных спектров стимулировали создание и дальнейшее бурное развитие квантовой теории и экспериментальных исследований квантовых явлений.

Уже в 1926 году Эрвин Шредингер сформулировал свое знаменитое волновое уравнение, а Энрико Ферми и Поль Дирак получили квантово-статистическое распределение для электронного газа, учитывающее заполнение отдельных квантовых состояний.

В 1928 году Феликс Блох произвел анализ квантово-механической задачи о движении электрона во внешнем периодическом поле кристаллической решетки и показал, что электронный энергетический спектр в кристаллическом твердом теле имеет зонную структуру. Фактически это стало началом нового направления в физике — теории твердого тела.

Весь XX век — это период интенсивного развития квантовой физики и всех тех разделов физики, для которых квантовая теория стала прародителем.

Появление квантовых вычислений

Идея использования квантовых вычислений впервые была высказана советским математиком Ю.И. Маниным в 1980 году в его знаменитой монографии «Вычислимое и невычислимое». Правда, интерес к его труду возник лишь два года спустя, в 1982 году, после опубликования статьи на ту же тему американского физика-теоретика нобелевского лауреата Ричарда Фейнмана. Он заметил, что определенные квантово-механические операции нельзя в точности переносить на классический компьютер. Это наблюдение привело его к мысли, что подобные вычисления могут быть более эффективными, если их осуществлять при помощи квантовых операций.

Рассмотрим, к примеру, квантово-механическую задачу об изменении состояния квантовой системы, состоящей из n спинов, за определенный промежуток времени. Не вникая в подробности математического аппарата квантовой теории, отметим, что общее состояние системы из n спинов описывается вектором в 2ⁿ-мерном комплексном пространстве, а изменение ее состояния — унитарной матрицей размером 2ⁿx2ⁿ. Если рассматриваемый промежуток времени очень мал, то матрица устроена очень просто и каждый из ее элементов легко вычислить, зная взаимодействие между спинами. Если же необходимо узнать изменение состояния системы за большой промежуток времени, то нужно перемножать такие матрицы, причем для этого требуется экспоненциально большое количество операций. Опять мы сталкиваемся с PN-полной задачей, нерешаемой за полиномиальное время на классических компьютерах. В настоящее время способа упростить данное вычисление не существует, и, скорее всего, моделирование квантовой механики является экспоненциально сложной математической задачей. Но если классические компьютеры не способны решать квантовые задачи, то, возможно, для этого целесообразно использовать саму квантовую систему? И если это действительно возможно, то подходят ли квантовые системы для решения других вычислительных задач? Подобные вопросы как раз и рассматривались Фейнманом и Маниным.

Уже в 1985 году Дэвид Дойч предложил конкретную математическую модель квантовой машины.

Однако вплоть до середины 90-х годов направление квантовых вычислений развивалось довольно вяло. Практическая реализация квантовых компьютеров оказалась весьма сложной. К тому же в научном сообществе с пессимизмом относились к тому, что квантовые операции способны ускорить решение определенных вычислительных задач. Так продолжалось вплоть до 1994 года, когда американский математик Питер Шор предложил для квантового компьютера алгоритм разложения n-значного числа на простые множители за время, полиномиально зависящее от n (квантовый алгоритм факторизации). Квантовый алгоритм факторизации Шора стал одним из основных факторов, приведших к интенсивному развитию квантовых методов вычислений и появлению алгоритмов, позволяющих решать некоторые NP-проблемы.

Естественно, возникает вопрос: почему, собственно, предложенный Шором квантовый алгоритм факторизации привел к таким последствиям? Дело в том, что задача разложения числа на простые множители имеет прямое отношение к криптографии, в частности к популярным системам шифрования RSA. Благодаря возможности разложения числа на простые множители за полиномиальное время квантовый компьютер теоретически позволяет расшифровывать сообщения, закодированные при помощи многих популярных криптографических алгоритмов, таких как RSA. До сих пор этот алгоритм считался сравнительно надежным, так как эффективный способ разложения чисел на простые множители для классического компьютера в настоящее время неизвестен. Шор придумал квантовый алгоритм, позволяющий разложить на простые множители n-значное число за n³(log n)^k шагов (k = const). Естественно, практическая реализация такого алгоритма могла иметь скорее негативные, чем позитивные последствия, поскольку позволяла подбирать ключи к шифрам, подделывать электронные подписи и т.п. Впрочем, до практической реализации настоящего квантового компьютера еще далеко, а потому в течение ближайших десяти лет можно не опасаться, что шифры могут быть взломаны с помощью квантовых компьютеров.

Идея квантовых вычислений

Итак, после краткого описания истории квантовых вычислений можно перейти к рассмотрению самой их сути. Идея (но не ее реализация) квантовых вычислений достаточно проста и интересна. Но даже для ее поверхностного понимания необходимо ознакомиться с некоторыми специфическими понятиями квантовой физики.

Прежде чем рассматривать обобщенные квантовые понятия вектора состояния и принципа суперпозиции, разберем простой пример поляризованного фотона. Поляризованный фотон — это пример двухуровневой квантовой системы. Состояние поляризации фотона можно задать вектором состояния, определяющим направление поляризации. Поляризация фотона может быть направлена вверх или вниз, поэтому говорят о двух основных, или базисных, состояниях, которые обозначают как |1 и |0.

Данные обозначения (бра/кэт-обозначения) были введены Дираком и имеют строго математическое определение (векторы базисных состояний), которое обусловливает правила работы с ними, однако, дабы не углубляться в математические дебри, мы не станем детально рассматривать эти тонкости.

Возвращаясь к поляризованному фотону, отметим, что в качестве базисных состояний можно было бы выбрать не только горизонтальное и вертикальное, но и любые взаимно ортогональные направления поляризации. Смысл базисных состояний заключается в том, что любая произвольная поляризация может быть выражена как линейная комбинация базисных состояний, то есть a|1+b|0. Поскольку нас интересует только направление поляризации (величина поляризации не важна), то вектор состояния можно считать единичным, то есть |a|²+|b|² = 1.

Теперь обобщим пример с поляризацией фотона на любую двухуровневую квантовую систему.

Предположим, имеется произвольная двухуровневая квантовая система, которая характеризуется базисными ортогональными состояниями |1 и |0. Согласно законам (постулатам) квантовой механики (принцип суперпозиции) возможными состояниями квантовой системы будут также суперпозиции y =  a|1+b|0, где a и b — комплексные числа, называемые амплитудами. Отметим, что аналога состояния суперпозиции в классической физике не существует.

Один из фундаментальных постулатов квантовой механики утверждает, что для того, чтобы измерить состояние квантовой системы, нужно ее разрушить. То есть любой процесс измерения в квантовой физике нарушает первоначальное состояние системы и переводит ее в новое состояние. Понять это утверждение не так-то просто, а потому остановимся на нем более подробное.

Вообще, понятие измерения в квантовой физике играет особую роль, и не стоит рассматривать его как измерение в классическом понимании. Измерение квантовой системы происходит всякий раз, когда она приходит во взаимодействие с «классическим» объектом, то есть с объектом, подчиняющимся законам классической физики. В результате такого взаимодействия состояние квантовой системы изменяется, причем характер и величина этого изменения зависят от состояния квантовой системы и потому могут служить его количественной характеристикой.

В связи с этим классический объект обычно называют прибором, а о его процессе взаимодействия с квантовой системой говорят как об измерении. Необходимо подчеркнуть, что при этом отнюдь не имеется в виду процесс измерения, в котором участвует наблюдатель. Под измерением в квантовой физике подразумевается всякий процесс взаимодействия между классическим и квантовым объектами, происходящий помимо и независимо от какого-либо наблюдателя. Выяснение роли измерения в квантовой физике принадлежит Нильсу Бору.

Итак, чтобы измерить квантовую систему, необходимо каким-то образом подействовать на нее классическим объектом, после чего ее первоначальное состояние будет нарушено. Кроме того, можно утверждать, что в результате измерения квантовая система будет переведена в одно из своих базисных состояний. К примеру, для измерения двухуровневой квантовой системы требуется как минимум двухуровневый классический объект, то есть классический объект, который может принимать два возможных значения: 0 и 1. В процессе измерения состояние квантовой системы будет преобразовано в один из базисных векторов, причем если при измерении классический объект принимает значение равное 0, то квантовый объект преобразуется к состоянию |0, а в случае если классический объект принимает значение равное 1, то квантовый объект преобразуется к состоянию |1.

Таким образом, хотя квантовая двухуровневая система может находиться в бесчисленном множестве состояний суперпозиции, но в результате измерения она принимает только одно из двух возможных базисных состояний. Квадрат модуля амплитуды |a|² определяет вероятность обнаружения (измерения) системы в базисном состоянии |1, а квадрат модуля амплитуды |b|² — в базисном состоянии |0.

Однако вернемся к нашему примеру с поляризованным фотоном. Для измерения состояния фотона (его поляризации) нам потребуется некоторое классическое устройство с классическим базисом {1,0}. Тогда состояние поляризации фотона a|1+b|0 будет определено как 1 (горизонтальная поляризация) с вероятностью |a|² и как 0 (вертикальная поляризация) с вероятностью |b|².

Поскольку измерение квантовой системы приводит ее к одному из базисных состояний и, следовательно, разрушает суперпозицию (к примеру, при измерении получается значение равное |1), то это означает, что в результате измерения квантовая система переходит в новое квантовое состояние и при следующем измерении мы получим значение |1 со стопроцентной вероятностью.

Вектор состояния двухуровневой квантовой системы называется также волновой функцией квантовых состояний y двухуровневой системы, или, в интерпретации квантовых вычислений, кубитом (quantum bit, qubit). В отличие от классического бита, который может принимать только два логических значения, кубит — это квантовый объект, и число его состояний, определяемых суперпозицией, неограниченно. Однако еще раз подчеркнем, что результат измерения кубита всегда приводит нас к одному из двух возможных значений.

Теперь рассмотрим систему из двух кубитов. Измерение каждого из них может дать значение классического объекта 0 или 1. Поэтому у системы двух кубитов имеется четыре классических состояния: 00, 01, 10 и 11. Аналогичные им базисные квантовые состояния: |00, |01, |10 и |11. Соответствующий вектор квантового состояния записывается в виде a|00+ b|01+ c|10+ d|11, где |a|² — вероятность при измерении получить значение 00, |b|² — вероятность получить значение 01 и т.д.

В общем случае если квантовая система состоит из L кубитов, то у нее имеется 2^L возможных классических состояний, каждое из которых может быть измерено с некоторой вероятностью. Функция состояния такой квантовой системы запишется в виде:

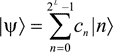
где |n — базисные квантовые состояния (например, состояние |001101, а |c_n|² — вероятность нахождения в базисном состоянии |n.

Для того чтобы изменить состояние суперпозиции квантовой системы, необходимо реализовать селективное внешнее воздействие на каждый кубит. С математической точки зрения такое преобразование представляется унитарными матрицами размера 2^Lx2^L. В результате будет получено новое квантовое состояние суперпозиции.

Структура квантового компьютера

Рассмотренное нами преобразование состояния суперпозиции квантовой системы, состоящей из L кубитов, по сути, представляет собой модель квантового компьютера. Рассмотрим, к примеру, более простой пример реализации квантовых вычислений. Допустим, имеется система из L кубитов, каждый из которых идеально изолирован от внешнего мира. В каждый момент времени мы можем выбрать произвольные два кубита и подействовать на них унитарной матрицей размером 4x4. Последовательность таких воздействий — это своего рода программа для квантового компьютера.

Чтобы использовать квантовую схему для вычисления, нужно уметь вводить входные данные, проделывать вычисления и считывать результат. Поэтому принципиальная схема любого квантового компьютера (см. рисунок) должна включать следующие функциональные блоки: квантовый регистр для ввода данных, квантовый процессор для преобразования данных и устройство для считывания данных.

Квантовый регистр представляет собой совокупность некоторого числа L кубитов. До ввода информации в компьютер все кубиты квантового регистра должны быть приведены в базисные состояния |0. Эта операция называется подготовкой, или инициализацией. Далее определенные кубиты (не все) подвергаются селективному внешнему воздействию (например, с помощью импульсов внешнего электромагнитного поля, управляемых классическим компьютером), которое изменяет значение кубитов, то есть из состояния |0 они переходят в состояние |1. При этом состояние всего квантового регистра перейдет в суперпозицию базисных состояний |nс, то есть состояние квантового регистра в начальный момент времени будет определяться функцией:

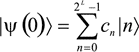
Понятно, что данное состояние суперпозиции можно использовать для бинарного (двоичного) представления числа n.

В квантовом процессоре введенные данные подвергаются последовательности квантовых логических операций, которые с математической точки зрения описываются унитарным преобразованием , действующим на состояние всего регистра. В результате через некоторое количество тактов работы квантового процессора исходное квантовое состояние системы становится новой суперпозицией вида:

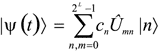
Говоря о квантовом процессоре, нужно сделать одно важное замечание. Оказывается, для построения любого вычисления достаточно всего двух базовых логических булевых операций. С помощью базовых квантовых операций можно имитировать работу обычных логических элементов, из которых сделаны компьютеры. Поскольку законы квантовой физики на микроскопическом уровне являются линейными и обратимыми, то и соответствующие квантовые логические устройства, производящие операции с квантовыми состояниями отдельных кубитов (квантовые вентили), оказываются логически и термодинамически обратимыми. Квантовые вентили аналогичны соответствующим обратимым классическим вентилям, но, в отличие от них, способны совершать унитарные операции над суперпозициями состояний. Выполнение унитарных логических операций над кубитами предполагается осуществлять с помощью соответствующих внешних воздействий, которыми управляют классические компьютеры.

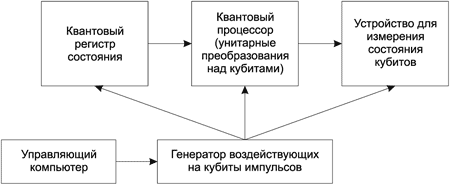
Схематическая структура квантового компьютера

После реализации преобразований в квантовом компьютере новая функция суперпозиции представляет собой результат вычислений в квантовом процессоре. Остается лишь считать полученные значения, для чего производится измерение значения квантовой системы. В итоге образуется последовательность нулей и единиц, причем, в силу вероятностного характера измерений, она может быть любой. Таким образом, квантовый компьютер может с некоторой вероятностью дать любой ответ. При этом квантовая схема вычислений считается правильной, если правильный ответ получается с вероятностью, достаточно близкой к единице. Повторив вычисления несколько раз и выбрав тот ответ, который встречается наиболее часто, можно снизить вероятность ошибки до сколь угодно малой величины.

Для того чтобы понять, чем различаются в работе классический и квантовый компьютеры, давайте вспомним, что классический компьютер хранит в памяти L бит, которые за каждый такт работы процессора подвергаются изменению. В квантовом компьютере в памяти (регистр состояния) хранятся значения L кубитов, однако квантовая система находится в состоянии, являющемся суперпозицией всех базовых 2L состояний, и изменение квантового состояния системы, производимое квантовым процессором, касается всех 2L базовых состояний одновременно. Соответственно в квантовом компьютере вычислительная мощность достигается за счет реализации параллельных вычислений, причем теоретически квантовый компьютер может работать в экспоненциальное число раз быстрее, чем классическая схема.

Считается, что для реализации полномасштабного квантового компьютера, превосходящего по производительности любой классический компьютер, на каких бы физических принципах он ни работал, следует обеспечить выполнение следующих основных требований:

• физическая система, представляющая собой полномасштабный квантовый компьютер, должна содержать достаточно большое число L>103 хорошо различимых кубитов для выполнения соответствующих квантовых операций;
• необходимо обеспечить максимальное подавление эффектов разрушения суперпозиции квантовых состояний, обусловленных взаимодействием системы кубитов с окружающей средой, в результате чего может стать невозможным выполнение квантовых алгоритмов. Время разрушения суперпозиции квантовых состояний (время декогерентизации) должно по крайней мере в 104 раз превышать время выполнения основных квантовых операций (время такта). Для этого система кубитов должна быть довольно слабо связана с окружением;
• необходимо обеспечить измерение с достаточно высокой надежностью состояния квантовой системы на выходе. Измерение конечного квантового состояния является одной из основных проблем квантовых вычислений.

Практическое применение квантовых компьютеров

Для практического применения пока не создано ни одного квантового компьютера, который бы удовлетворял всем вышеперечисленным условиям. Однако во многих развитых странах разработке квантовых компьютеров уделяется пристальное внимание и в такие программы ежегодно вкладываются десятки миллионов долларов.

На данный момент наибольший квантовый компьютер составлен всего из семи кубитов. Этого достаточно, чтобы реализовать алгоритм Шора и разложить число 15 на простые множители 3 и 5.

Если же говорить о возможных моделях квантовых компьютеров, то их, в принципе, довольно много. Первый квантовый компьютер, который был создан на практике, — это импульсный ядерный магнитно-резонансный (ЯМР) спектрометр высокого разрешения, хотя он, конечно же, как квантовый компьютер не рассматривался. Лишь когда появилась концепция квантового компьютера, ученые поняли, что ЯМР-спектрометр представляет собой вариант квантового компьютера.

В ЯМР-спектрометре спины ядер исследуемой молекулы образуют кубиты. Каждое ядро имеет свою частоту резонанса в данном магнитном поле. При воздействии импульсом на ядро на его резонансной частоте оно начинает эволюционировать, остальные же ядра не испытывают никакого воздействия. Для того чтобы заставить эволюционировать другое ядро, нужно взять иную резонансную частоту и дать импульс на ней. Таким образом, импульсное воздействие на ядра на резонансной частоте представляет собой селективное воздействие на кубиты. При этом в молекуле есть прямая связь между спинами, поэтому она является идеальной заготовкой для квантового компьютера, а сам спектрометр представляет собой квантовый процессор.

Первые эксперименты на ядерных спинах двух атомов водорода в молекулах 2,3-дибромотиофена SCH:(CBr)₂:CH и на трех ядерных спинах — одном в атоме водорода H и двух в изотопах углерода ¹³C в молекулах трихлорэтилена CCl₂:CHCl — были поставлены в 1997 году в Оксфорде (Великобритания).

В случае использования ЯМР-спектрометра важно, что для селективного воздействия на ядерные спины молекулы необходимо, чтобы они заметно различались по резонансным частотам. Позднее были осуществлены квантовые операции в ЯМР-спектрометре с числом кубитов 3, 5, 6 и 7.

Главным преимуществом ЯМР-спектрометра является то, что в нем можно использовать огромное количество одинаковых молекул. При этом каждая молекула (точнее, ядра атомов, из которых она состоит) представляет собой квантовую систему. Последовательности радиочастотных импульсов, выполняющие роль определенных квантовых логических вентилей, осуществляют унитарные преобразования состояний соответствующих ядерных спинов одновременно для всех молекул. То есть селективное воздействие на отдельный кубит заменяется одновременным обращением к соответствующим кубитам во всех молекулах большого ансамбля. Компьютер такого рода получил название ансамблевого (bulk-ensemble quantum computer) ЯМР квантового компьютера. Такие компьютеры могут работать при комнатной температуре, а время декогерентизации квантовых состояний ядерных спинов составляет несколько секунд.

В области ЯМР квантовых компьютеров на органических жидкостях к настоящему времени достигнуты наибольшие успехи. Они обусловлены в основном хорошо развитой импульсной техникой ЯМР-спектроскопии, обеспечивающей выполнение различных операций над когерентными суперпозициями состояний ядерных спинов, и возможностью использования для этого стандартных ЯМР-спектрометров, работающих при комнатной температуре.

Основным ограничением ЯМР квантовых компьютеров является сложность инициализации начального состояния в квантовом регистре. Дело в том, что в большом ансамбле молекул исходное состояние кубитов различно, что осложняет приведение системы к начальному состоянию.

Другое ограничение ЯМР квантовых компьютеров связано с тем, что измеряемый на выходе системы сигнал экспоненциально убывает с ростом числа кубитов L. Кроме того, число ядерных кубитов в отдельной молекуле с сильно различающимися резонансными частотами ограничено. Это приводит к тому, что ЯМР квантовые компьютеры не могут иметь больше десяти кубитов. Их следует рассматривать лишь как прототипы будущих квантовых компьютеров, полезные для отработки принципов квантовых вычислений и проверки квантовых алгоритмов.

Другой вариант квантового компьютера основан на использовании ионных ловушек, когда в роли кубитов выступает уровень энергии ионов, захваченных ионными ловушками, которые создаются в вакууме определенной конфигурацией электрического поля в условиях лазерного охлаждения их до сверхнизких температур. Первый прототип квантового компьютера, основанного на этом принципе, был предложен в 1995 году. Преимущество такого подхода состоит в сравнительно простом индивидуальном управлении отдельными кубитами. Основными недостатками квантовых компьютеров этого типа являются необходимость создания сверхнизких температур, обеспечение устойчивости состояния ионов в цепочке и ограниченность возможного числа кубитов — не более 40.

Возможны и другие схемы квантовых компьютеров, разработка которых ведется в настоящее время. Однако пройдет еще как минимум десять лет, прежде чем настоящие квантовые компьютеры наконец будут созданы.

КомпьютерПресс 5'2007