Блеск и нищета сводных таблиц
Часть 11
Предыдущие статьи данного цикла были посвящены возможностям операторов семейства КУБ(), позволяющих выполнять MDX-вычисления в программе MS Excel. В отдельном материале рассказывалось об измерении Account, выступающем в роли фундамента для большинства современных финансовых приложений.
В настоящей статье рассматриваются операции, которые, условно говоря, являются обратными к функциям КУБ(). Мы обсудим, каким образом функции листа Microsoft Excel запускаются на стороне OLAP-сервера. У читателей может возникнуть резонный вопрос: в чем заключается практическая ценность данного умения? Иными словами, стоит ли игра свеч? Ответ на него не столь тривиален, как кажется на первый взгляд. В настоящее время в Microsoft Analysis содержится обширная библиотека MDX-функций, удовлетворяющая большую часть типовых потребностей при работе с многомерными данными. При этом наряду со специфическими функциями, предназначенными для обработки наборов, иерархий или уровней в OLAP-сервере, реализованы практически все стандартные числовые функции, а также многие операторы для выполнения статистического анализа данных (расчет медианы распределения, вычисление параметров линейной регрессии и т.п.).
Однако на практике с завидной регулярностью встречаются задачи, для решения которых недостаточно даже столь обширных возможностей. К ним, в частности, относятся прикладные расчеты из области финансов. Рассмотрим для примера показатель NPV (чистый дисконтированный денежный поток), характеризующий качество инвестиционных проектов. Он представляет собой число, которое является суммой ряда:
Формула 1
![]()
Сразу отметим, что среди базового набора MDX-операторов нет функции для определения NPV. Вычислять же подобную сумму в виде формулы, как суперпозицию элементарных функций MDX, неудобно по целому ряду причин. Кроме сложности алгоритма, серьезным ограничением является сама среда аналитического сервера, которая является декларативной по своей сути. Вследствие этого расчеты, основанные на процедурной логике (представляющие собой последовательность из этапов вычислений), часто не могут быть реализованы в виде MDX-выражений.
В Microsoft Excel ситуация с экономическими вычислениями намного лучше. Являясь универсальной программой для бизнес-расчетов, Microsoft Excel содержит огромное число функций на все случаи жизни, в том числе целый класс (больше 30) различных экономических операторов. Данные функции автоматизируют вычисление типовых финансовых показателей. При этом для пользователя расчет сводится к единственной операции — корректному заданию аргументов. Так, для вычисления дисконтированного денежного потока в соответствии с формулой 1 пользователю достаточно воспользоваться специальной функцией ЧПС() (русскоязычный аналог функции NPV()), определив в ней исходные параметры: ставку дисконтирования, а также ненормированные значения денежного потока по периодам (рис. 1).
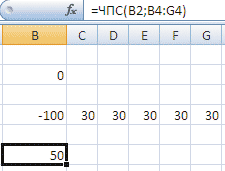
Рис. 1. Расчет показателя NPV()
в среде Microsoft Excel
Финансовые функции из программы Microsoft Excel, как, впрочем, и функции из других разделов, уже давно являются общепринятым стандартом. Они удобны в использовании и, что особенно важно, изначально знакомы большинству пользователей. Поэтому возможность их вызова при составлении MDX-выражения весьма привлекательна.
Описанная выше проблема в Microsoft Analysis решается тем же способом, что и в случае с SQL Server, — посредством вызова внешних хранимых процедур. Такие процедуры добавляются путем развертывания на сервере соответствующих COM- или CLR-сборок. Читателям, интересующимся технической стороной вопроса, рекомендую материал, изложенный в классической книге по аналитическому серверу «Microsoft SQL Server 2005 Analysis Services. OLAP и многомерный анализ данных» (под общей редакцией А.Бергера и И.Горбач).
Мы же рассмотрим частный случай, когда на сервере с Microsoft Analysis устанавливается офисный пакет Microsoft Office. В ходе установки в разделе Assemblies (Сборки) аналитического сервера регистрируется новая COM-сборка ExcelMDX (рис. 2).
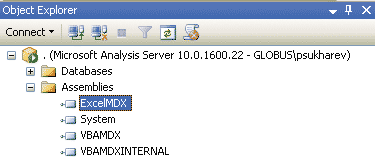
Рис. 2. Подключение сборки ExcelMDX
Процесс регистрации сборки ExcelMDX происходит в автоматическом режиме и не требует участия пользователя, после его завершения на стороне OLAP-сервера можно сразу применять функции листа из программы Microsoft Excel. Покажем, как это делается. Для начала напишем следующий код:
Выражение 1
with
member measures.NPV as Excel.NPV(0,-100,30,30,30,30,30)
select measures.NPV on 0
from [PF]
Выражение 1 определяет на оси Measures новый вычисляемый элемент NPV, рассчитывающий значение дисконтированного денежного потока при помощи функции NPV() из среды Microsoft Excel. Заметим, что для вызова оператора NPV() в MDX-запросе перед ним необходимо проставить префикс Excel.
Из рис. 3 видно, что при заданных начальных условиях оператор Excel.NPV() возвращает значение, равное 50.

Рис. 3. Расчет показателя NPV()
в среде Microsoft Analysis
Данный факт не может не радовать — полученная величина в точности совпадает со значением функции ЧПС() из начала статьи. Но для достижения полноценного результата нужно уметь делать немного больше — необходимо научиться передавать на вход внешней функции Excel.NPV() в качестве аргументов элементы многомерного пространства. Данный этап сопряжен с определенными трудностями, о которых в большинстве справочных изданий напрямую не рассказывается. Далее он будет подробно рассмотрен.
Сначала проведем небольшую подготовительную работу. Создадим в многомерном пространстве набор, имитирующий денежный поток из нашего примера (рис. 4).

Рис. 4. Имитация денежного потока
в многомерном пространств
Набор, показанный на рис. 4, формально задается следующим множеством кортежей:
Набор 1
{
([Янв], [Дир_2],[LE],[Факт],[Установочная плата],[Сумма]),
([Фев], [Дир_2],[LE],[Факт],[Установочная плата],[Сумма]),
([Мар], [Дир_2],[LE],[Факт],[Установочная плата],[Сумма]),
([Апр], [Дир_2],[LE],[Факт],[Установочная плата],[Сумма]),
([Май], [Дир_2],[LE],[Факт],[Установочная плата],[Сумма]),
([Июн], [Дир_2],[LE],[Факт],[Установочная плата],[Сумма])
}
Попытка указать данное множество в качестве аргумента для функции Excel.NPV() приводит к ошибке ее исполнения (рис. 5).
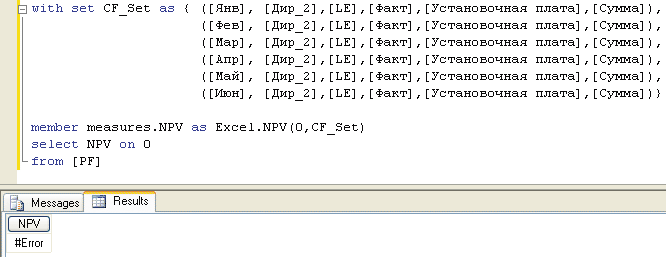
Рис. 5. Некорректный вызов внешней процедуры
В этом нет ничего удивительного. Функция Excel.NPV(), будучи вызванной на стороне аналитического сервера, выполняется во внешней программе — Microsoft Excel, которая ничего не знает о многомерных пространствах и наборах, состоящих из кортежей.
Однако указание координат из нескольких измерений в наборе 1 требуется лишь для выбора в определенном порядке шести конкретных числовых значений на оси меры [Сумма]. Элементы, расположенные на единственной оси мер, без привязки к измерениям куба, можно с успехом считать обычным числовым массивом. А числовые массивы программе Microsoft Excel знакомы хорошо. Поэтому исходная задача сводится к преобразованию многокоординатного набора в одномерный числовой массив. Для таких случаев в библиотеке операторов MDX предусмотрена специальная функция SetToArray(), имеющая довольно лаконичный синтаксис:
Выражение 2
SetToArray(Set_Expression1 [ ,Set_Expression2,...n ][ ,Numeric_Expression ])
Аргументами данной функции являются многомерные выражения Set_Expression1,…n, возвращающие наборы, а также выражение Numeric_Expression, возвращающее число. За внешней простотой записи скрываются мощные возможности, очень полезные на практике. В качестве первого шага подставим набор 1 в функцию SetToArray() (рис. 6).
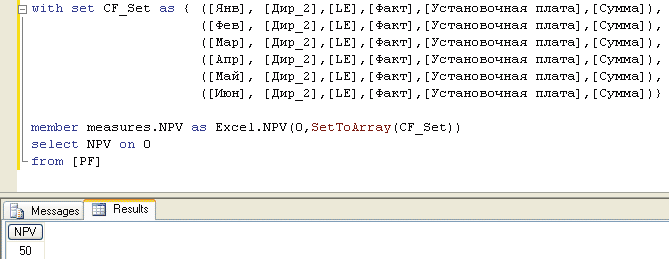
Рис. 6. Использование функции SetToArray()
Как видно из рис. 6, использование вложенной функции SetToArray() исправляет возникавшую ранее ошибку исполнения MDX-выражения — вычисляемый элемент NPV начинает корректно рассчитываться.
Недостатком предложенного решения является громоздкая форма записи исходного набора. К счастью, посредством операции перекрестного объединения множеств он представляется и в более компактном виде:
Выражение 3
{{[Янв],[Фев],[Мар],[Апр],[Май],[Июн]}*[Дир_2]*[LE]*[Факт]*[Установочная плата]*[Сумма]}
В свою очередь, набор из выражения 3 можно по-разному указывать в MDX-запросе. Первый способ заключается в создании промежуточного именованного множества с помощью инструкции WITH SET (рис. 7).
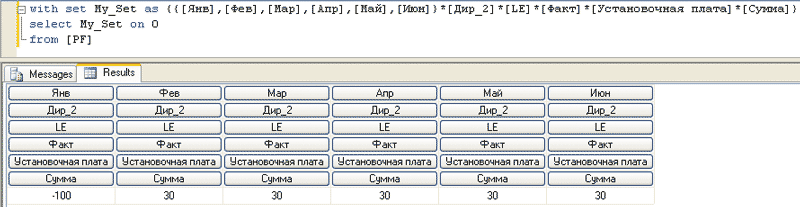
Рис. 7. Создание набора посредством инструкции WITH SET
Альтернативный вариант — сформировать нужное множество «на лету», прямо внутри оператора Select (рис. 8).
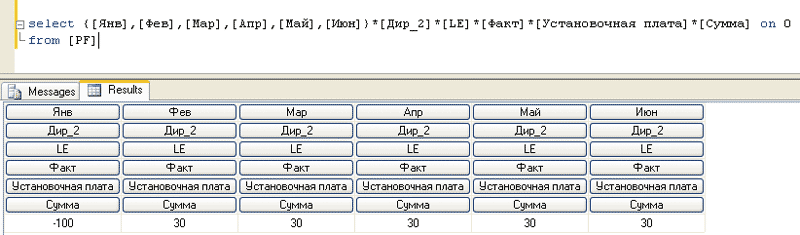
Рис. 8. Определение набора в операторе Select
Какой из двух подходов выбрать — во многом дело вкуса разработчика. Но функция SetToArray() позволяет при желании использовать любой из них. Первый прием, основанный на создании промежуточного набора, был продемонстрирован выше. Второй вариант, базирующийся на непосредственном определении прямого произведения, реализуется еще проще — нужные множества перечисляются в качестве аргументов функции SetToArray() (рис. 9).
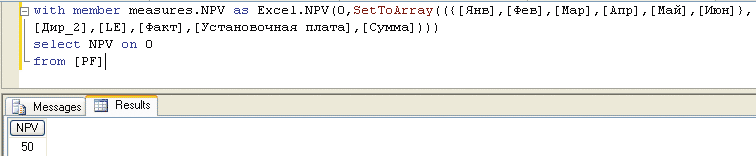
Рис. 9. Определение прямого произведения множеств в функции SetToArray()
Набор из выражения 3 обладает очевидным преимуществом — его легко ассоциировать с одномерным массивом. Действительно, если все измерения, кроме одного, представлены единственным элементом, то их можно указывать в выходном наборе произвольным образом. Результат всегда будет одинаковым: сначала выбирается соответствующая проекция для элемента [Янв], затем для элемента [Фев] и т.д. Но ситуация резко осложняется, когда сразу несколько измерений содержат больше одного элемента. В этом случае порядок перечисления измерений в наборе становится важным, так как он определяет последовательность выбора элементов на оси Measures. А это, в свою очередь, существенно влияет на работу функции SetToArray().
Расширим набор из начала статьи новым значением [Абонентская плата] на оси измерений [Сервис]:
Набор 2
{ [Янв], [Фев], [Мар], [Апр], [Май], [Июн] } * [Дир_2] * { [Установочная плата], [Абонентская плата] } * [Сумма] * [LE] * [Факт].
Рассчитаем для нового набора значение показателя NPV (рис. 10).

Рис. 10. Расчет NPV для набора, в котором измерение [Дата] стоит перед измерением [Сервис]
Нас интересует принцип работы оператора SetToArray(). Проще говоря, по какому правилу элементы из набора 2 добавляются в выходной массив. Обратите внимание, что в исходном наборе измерение [Месяц] стоит перед измерением [Сервис]. Соответственно массив должен составляться «в помесячной разбивке» — содержать сначала все элементы, относящиеся к проекции куба по месяцу [Янв], затем элементы из проекции по месяцу [Фев] и т.д. Подходящим графическим образом для набора 2 будет таблица, показанная на рис. 11.
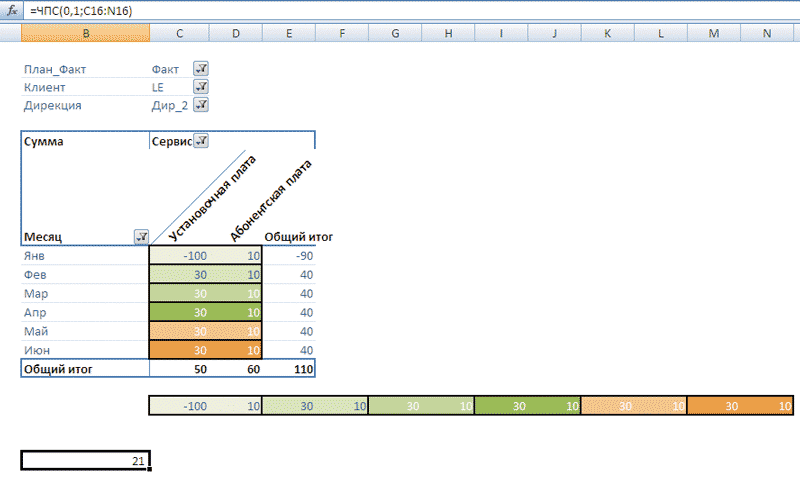
Рис. 11. Таблица для набора, в котором измерение [Дата] стоит перед измерением [Сервис]
Если говорить о работе функции SetToArray() в категориях рис. 11, то она фактически заключается в построчном выборе значений из таблицы и их последующем размещении друг за другом в одну строку. Итоговый результат представлен на рис. 11 диапазоном С16:N16. Если теперь этот диапазон указать в качестве аргумента для функции листа NPV() с коэффициентом дисконтирования «0,1», то мы получим значение, равное 21. Оно совпадает с величиной показателя, рассчитанного ранее внутри аналитического куба.
Теперь на базе набора 2 создадим новый набор — переставим в операторе перекрестного умножения множеств измерения [Time] и [Сервис]:
Набор 3
{ [Установочная плата], [Абонентская плата] } * [Дир_2] * { [Янв], [Фев], [Мар], [Апр], [Май], [Июн] } * [Сумма] * [LE] * [Факт].
С позиций многомерного анализа наборы являются тождественными друг другу — определяют одну область многомерного пространства. Однако использование нового набора в функции SetToArray() приводит к изменению значения показателя NPV (рис. 12).

Рис. 12. Расчет NPV для набора, в котором измерение [Дата] стоит после измерения [Сервис]
Ответить на вопрос, почему так происходит, нам поможет еще одна иллюстрация. В наборе 3 измерение [Сервис] стоит перед измерением [Месяц]. Функция SetToArray() генерирует массив уже не в «помесячной», а в «постатейной разбивке» — сначала перечисляются элементы, относящиеся к проекции куба по услуге [Установочная плата], затем — к проекции по услуге [Абонентская плата]. Набор 3 представляется таблицей, изображенной на рис. 13.
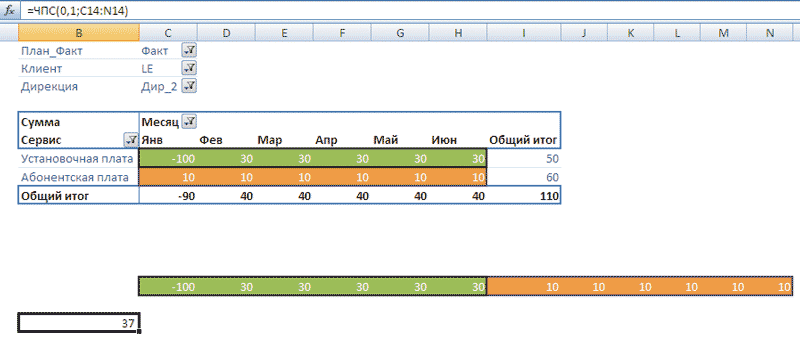
Рис. 13. Таблица для набора, в котором измерение [Дата] стоит после измерения [Сервис]
Из рисунков видно, что обе таблицы содержат равное количество ячеек, причем их значения совпадают для одинаковых координат пространства. Таблицы представляют одну область многомерного пространства, о чем мы уже писали. В то же время таблицы различаются своими линейными размерами — ((6×2) против (2×6)), а также взаимным расположением ячеек. Работа функции SetToArray() заключается в построчном выборе значений из таблицы и расстановке их друг за другом в одну строку. На рис. 13 результат ее работы, как и в первый раз, представлен диапазоном С16:N16. Однако новый массив является уже другой перестановкой исходного множества значений, что в конечном счете влияет на величину показателя NPV().
Надеюсь, приведенных доводов достаточно, чтобы убедить читателей соблюдать особую осторожность при трансформации многомерных множеств. Последовательность обхода точек пространства, выполняемая функцией SetToArray(), довольна сложна для понимания, особенно в случае большого количества измерений с несколькими элементами. Вследствие этого получаемый результат часто существенно отличается от того, как представляет себе ситуацию бизнес-пользователь.
В настоящей статье хочется затронуть еще одну важную тему — организацию вычислений над элементами мер. Создание дополнительных показателей в процедурных средах, в частности в Microsoft Excel, не представляет особого труда. Достаточно сначала определить новую переменную, после чего присвоить ей некоторое значение. В Microsoft Excel расчетные показатели могут быть определены в любой свободной ячейке листа. Но в аналитических пространствах нет такого подходящего «свободного места», элементы должны быть обязательно жестко привязаны к одной из координатных осей. Создание вычисляемого элемента неизбежно влечет за собой расширение всего логического пространства, так как требует определения дополнительных координат. Понятно, что такой подход при решении частных прикладных задач не является оптимальным. В аналитическом сервере существуют различные механизмы, позволяющие управлять сроком жизни вычисляемых элементов. Более удобным видится перенос расчетов на сторону внешнего приложения, использующего OLAP-данные. Функция SetToArray() позволяет выполнить подобную операцию. Ее последний аргумент Numeric_Expression определяет MDX()-выражение, которое рассчитывается в момент формирования одномерного массива. Фактически это особого рода вычисляемый элемент, хранящийся вне аналитического пространства и никак не влияющий на его работу.
Начнем с простого поясняющего примера — немного модифицируем предыдущее выражение для расчета показателя NPV() (рис. 14).

Рис. 14. Использование константы в качестве Numeric_Expression
В MDX-выражении в параметре Numeric_Expression задана тривиальная формула, равная константе «1». Замена текущего значения меры на 1 выполняется для каждого элемента исходного набора. Учитывая, что он состоит из 12 членов, на выходе сформируется массив, состоящий из 12 единиц. Показатель NPV для такого диапазона при нулевой ставке дисконтирования равен 12, что мы видим на рисунке в качестве результирующего значения выражения.
Перейдем теперь к более сложному случаю. Предположим, мы хотим, чтобы показатель NPV считался для денежного потока, скорректированного с учетом сезонности. Другими словами, чтобы вместо существующей внутри куба меры [Сумма] использовалось аналитическое выражение вида [Сумма]*[Дата].[Дата].CurrentMember.Properties(‘SF’) (считаем, что нормировочные коэффициенты для сезонного фактора хранятся в свойстве SF измерения [Дата]). Для выполнения такой операции достаточно подставить MDX-выражение на место параметра Numeric_Expression функции SetToArray() (рис. 15).

Рис. 15. Добавление MDX-выражения в функцию SetToArray()
За лаконичной записью формулы стоит довольно сложный расчет. Понять его помогает рис. 16. Он показывает, какую последовательность операций в книге Excel необходимо выполнить для получения аналогичного результата.

Рис. 16. Иллюстрация расчета в среде Microsoft Excel
В завершении статьи сделаем еще одно замечание общего плана. Аналитический сервер поддерживает режим вложенных вызовов для внешних хранимых процедур, что в ряде случаев позволяет существенно повысить гибкость их использования. Для подтверждения данного тезиса доработаем выражение, показанное на рис. 12, таким образом, чтобы вычисленный результат округлялся до целых чисел. Задача округления значений, как правило, возникает на этапе представления результатов пользователю и обычно выполняется на стороне клиентского приложения. Поэтому в библиотеке базовых функций MDX нет специального оператора типа ROUND(). Соответственно если в ходе прикладных расчетов возникнет потребность в округлении значений, то для выполнения такой операции придется вызвать внешнюю функцию из программы Microsoft Excel (рис. 17).
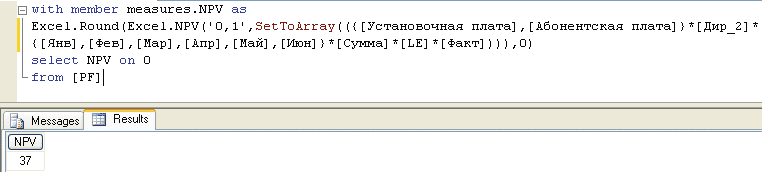
Рис. 17. Вложенный вызов внешних процедур
В статье был рассмотрен вопрос применения в среде Microsoft Analysis Services пользовательских функций из внешних приложений. Потребность в такой функциональности регулярно возникает на практике. В частности, выполнение на стороне сервера типовых экономических расчетов значительно упрощается за счет финансовых функций, встроенных в программу Microsoft Excel. Для преобразования многомерных данных в подходящий формат необходимо использовать одну из функций конвертации, например SetToArray().








